Sample Efficient Learning of Predictors that Complement Humans
Paper and Code
Jul 19, 2022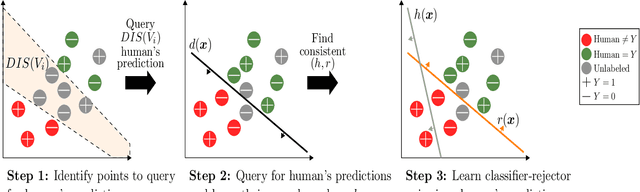
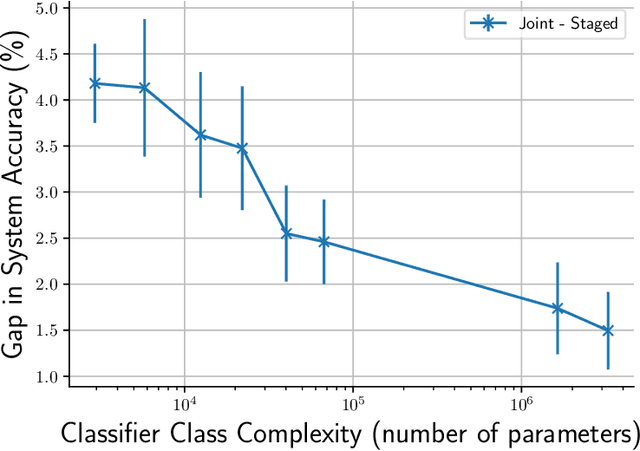
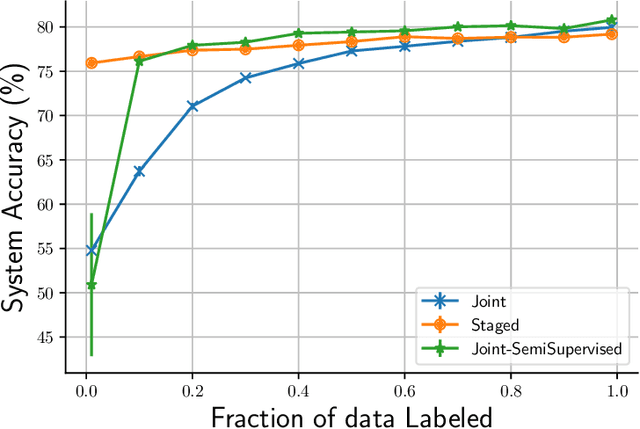
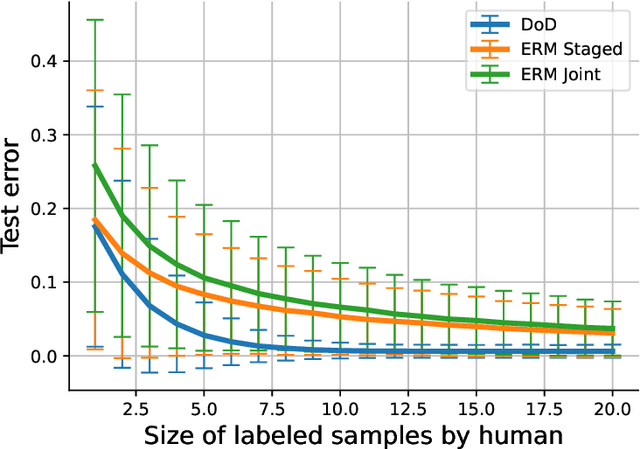
One of the goals of learning algorithms is to complement and reduce the burden on human decision makers. The expert deferral setting wherein an algorithm can either predict on its own or defer the decision to a downstream expert helps accomplish this goal. A fundamental aspect of this setting is the need to learn complementary predictors that improve on the human's weaknesses rather than learning predictors optimized for average error. In this work, we provide the first theoretical analysis of the benefit of learning complementary predictors in expert deferral. To enable efficiently learning such predictors, we consider a family of consistent surrogate loss functions for expert deferral and analyze their theoretical properties. Finally, we design active learning schemes that require minimal amount of data of human expert predictions in order to learn accurate deferral systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge