Stochastic Normalizing Flows
Paper and Code
Feb 19, 2020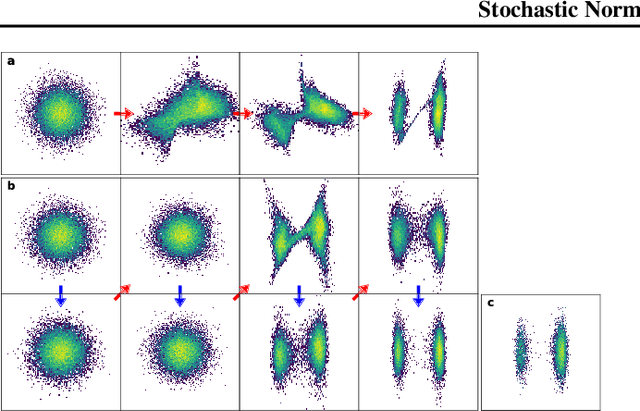
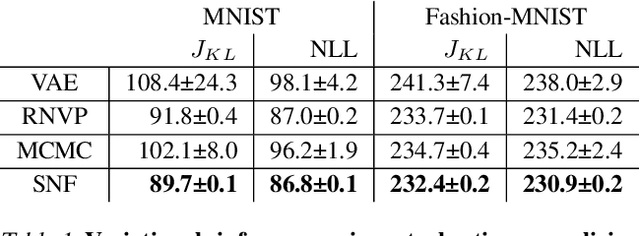

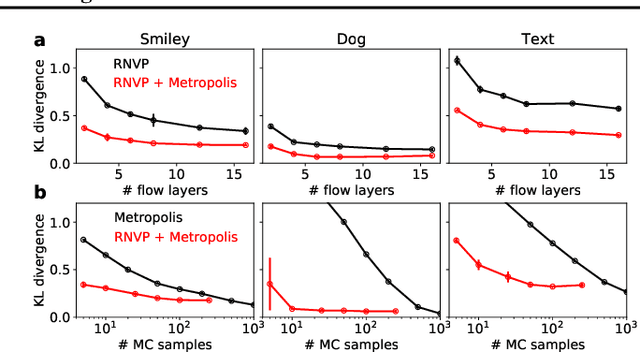
Normalizing flows are popular generative learning methods that train an invertible function to transform a simple prior distribution into a complicated target distribution. Here we generalize the framework by introducing Stochastic Normalizing Flows (SNF) - an arbitrary sequence of deterministic invertible functions and stochastic processes such as Markov Chain Monte Carlo (MCMC) or Langevin Dynamics. This combination can be powerful as adding stochasticity to a flow helps overcoming expressiveness limitations of a chosen deterministic invertible function, while the trainable flow transformations can improve the sampling efficiency over pure MCMC. Key to our approach is that we can match a marginal target density without having to marginalize out the stochasticity of traversed paths. Invoking ideas from nonequilibrium statistical mechanics, we introduce a training method that only uses conditional path probabilities. We can turn an SNF into a Boltzmann Generator that samples asymptotically unbiased from a given target density by importance sampling of these paths. We illustrate the representational power, sampling efficiency and asymptotic correctness of SNFs on several benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge