Equivariant Flows: sampling configurations for multi-body systems with symmetric energies
Paper and Code
Oct 02, 2019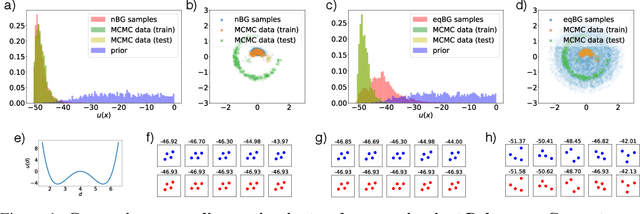
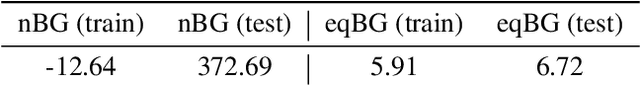
Flows are exact-likelihood generative neural networks that transform samples from a simple prior distribution to the samples of the probability distribution of interest. Boltzmann Generators (BG) combine flows and statistical mechanics to sample equilibrium states of strongly interacting many-body systems such as proteins with 1000 atoms. In order to scale and generalize these results, it is essential that the natural symmetries of the probability density - in physics defined by the invariances of the energy function - are built into the flow. Here we develop theoretical tools for constructing such equivariant flows and demonstrate that a BG that is equivariant with respect to rotations and particle permutations can generalize to sampling nontrivially new configurations where a nonequivariant BG cannot.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge