Decoupling Pixel Flipping and Occlusion Strategy for Consistent XAI Benchmarks

Feature removal is a central building block for eXplainable AI (XAI), both for occlusion-based explanations (Shapley values) as well as their evaluation (pixel flipping, PF). However, occlusion strategies can vary significantly from simple mean replacement up to inpainting with state-of-the-art diffusion models. This ambiguity limits the usefulness of occlusion-based approaches. For example, PF benchmarks lead to contradicting rankings. This is amplified by competing PF measures: Features are either removed starting with most influential first (MIF) or least influential first (LIF). This study proposes two complementary perspectives to resolve this disagreement problem. Firstly, we address the common criticism of occlusion-based XAI, that artificial samples lead to unreliable model evaluations. We propose to measure the reliability by the R(eference)-Out-of-Model-Scope (OMS) score. The R-OMS score enables a systematic comparison of occlusion strategies and resolves the disagreement problem by grouping consistent PF rankings. Secondly, we show that the insightfulness of MIF and LIF is conversely dependent on the R-OMS score. To leverage this, we combine the MIF and LIF measures into the symmetric relevance gain (SRG) measure. This breaks the inherent connection to the underlying occlusion strategy and leads to consistent rankings. This resolves the disagreement problem, which we verify for a set of 40 different occlusion strategies.

Multi-dimensional concept discovery (MCD): A unifying framework with completeness guarantees

The completeness axiom renders the explanation of a post-hoc XAI method only locally faithful to the model, i.e. for a single decision. For the trustworthy application of XAI, in particular for high-stake decisions, a more global model understanding is required. Recently, concept-based methods have been proposed, which are however not guaranteed to be bound to the actual model reasoning. To circumvent this problem, we propose Multi-dimensional Concept Discovery (MCD) as an extension of previous approaches that fulfills a completeness relation on the level of concepts. Our method starts from general linear subspaces as concepts and does neither require reinforcing concept interpretability nor re-training of model parts. We propose sparse subspace clustering to discover improved concepts and fully leverage the potential of multi-dimensional subspaces. MCD offers two complementary analysis tools for concepts in input space: (1) concept activation maps, that show where a concept is expressed within a sample, allowing for concept characterization through prototypical samples, and (2) concept relevance heatmaps, that decompose the model decision into concept contributions. Both tools together enable a detailed understanding of the model reasoning, which is guaranteed to relate to the model via a completeness relation. This paves the way towards more trustworthy concept-based XAI. We empirically demonstrate the superiority of MCD against more constrained concept definitions.

Reconstructing Kernel-based Machine Learning Force Fields with Super-linear Convergence

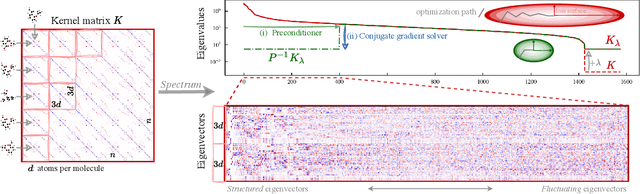
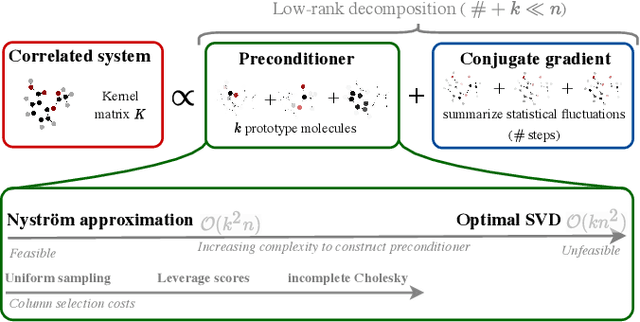
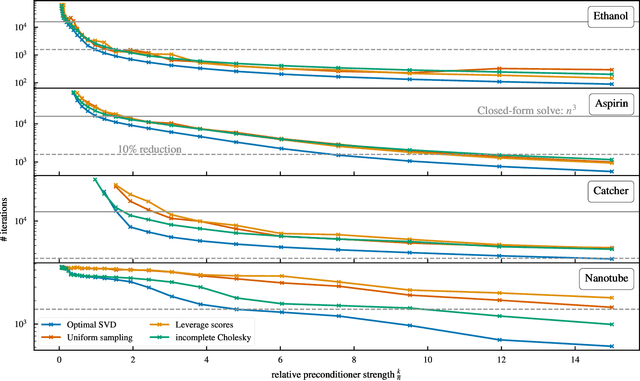
Kernel machines have sustained continuous progress in the field of quantum chemistry. In particular, they have proven to be successful in the low-data regime of force field reconstruction. This is because many physical invariances and symmetries can be incorporated into the kernel function to compensate for much larger datasets. So far, the scalability of this approach has however been hindered by its cubical runtime in the number of training points. While it is known, that iterative Krylov subspace solvers can overcome these burdens, they crucially rely on effective preconditioners, which are elusive in practice. Practical preconditioners need to be computationally efficient and numerically robust at the same time. Here, we consider the broad class of Nystr\"om-type methods to construct preconditioners based on successively more sophisticated low-rank approximations of the original kernel matrix, each of which provides a different set of computational trade-offs. All considered methods estimate the relevant subspace spanned by the kernel matrix columns using different strategies to identify a representative set of inducing points. Our comprehensive study covers the full spectrum of approaches, starting from naive random sampling to leverage score estimates and incomplete Cholesky factorizations, up to exact SVD decompositions.

Sparse Subspace Clustering for Concept Discovery (SSCCD)

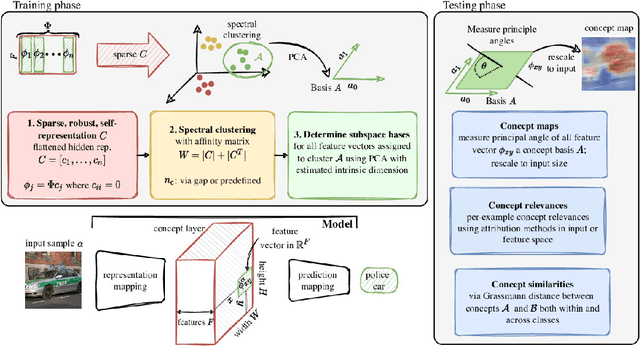
Concepts are key building blocks of higher level human understanding. Explainable AI (XAI) methods have shown tremendous progress in recent years, however, local attribution methods do not allow to identify coherent model behavior across samples and therefore miss this essential component. In this work, we study concept-based explanations and put forward a new definition of concepts as low-dimensional subspaces of hidden feature layers. We novelly apply sparse subspace clustering to discover these concept subspaces. Moving forward, we derive insights from concept subspaces in terms of localized input (concept) maps, show how to quantify concept relevances and lastly, evaluate similarities and transferability between concepts. We empirically demonstrate the soundness of the proposed Sparse Subspace Clustering for Concept Discovery (SSCCD) method for a variety of different image classification tasks. This approach allows for deeper insights into the actual model behavior that would remain hidden from conventional input-level heatmaps.

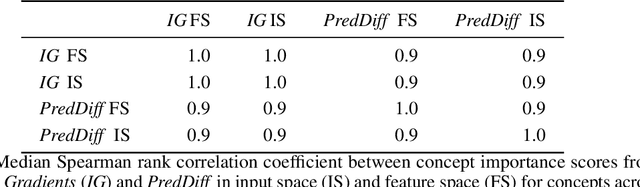
$PredDiff$: Explanations and Interactions from Conditional Expectations

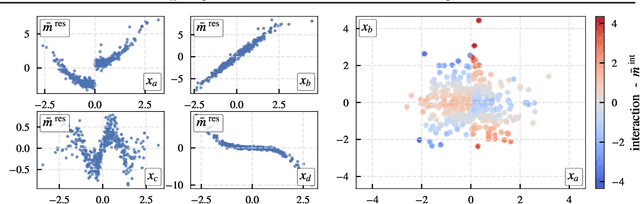
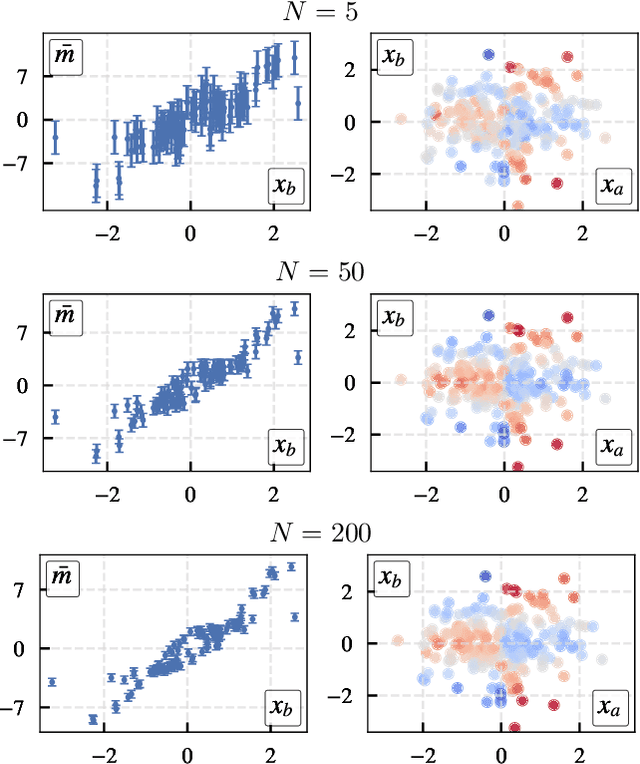
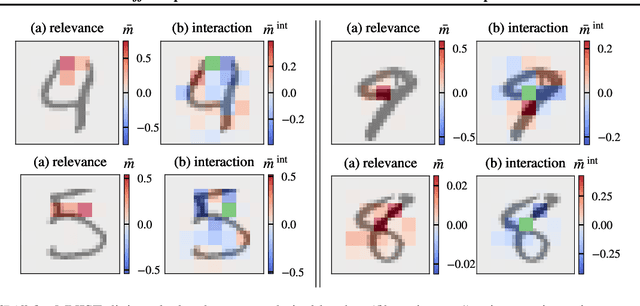
$PredDiff$ is a model-agnostic, local attribution method that is firmly rooted in probability theory. Its simple intuition is to measure prediction changes when marginalizing out feature variables. In this work, we clarify properties of $PredDiff$ and put forward several extensions of the original formalism. Most notably, we introduce a new measure for interaction effects. Interactions are an inevitable step towards a comprehensive understanding of black-box models. Importantly, our framework readily allows to investigate interactions between arbitrary feature subsets and scales linearly with their number. We demonstrate the soundness of $PredDiff$ relevances and interactions both in the classification and regression setting. To this end, we use different analytic, synthetic and real-world datasets.