$PredDiff$: Explanations and Interactions from Conditional Expectations
Paper and Code
Feb 26, 2021
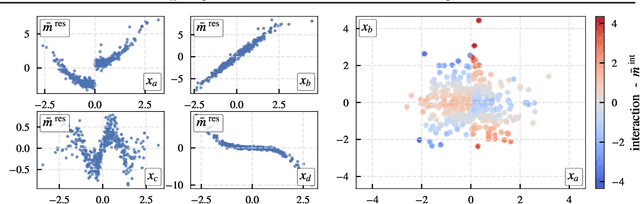
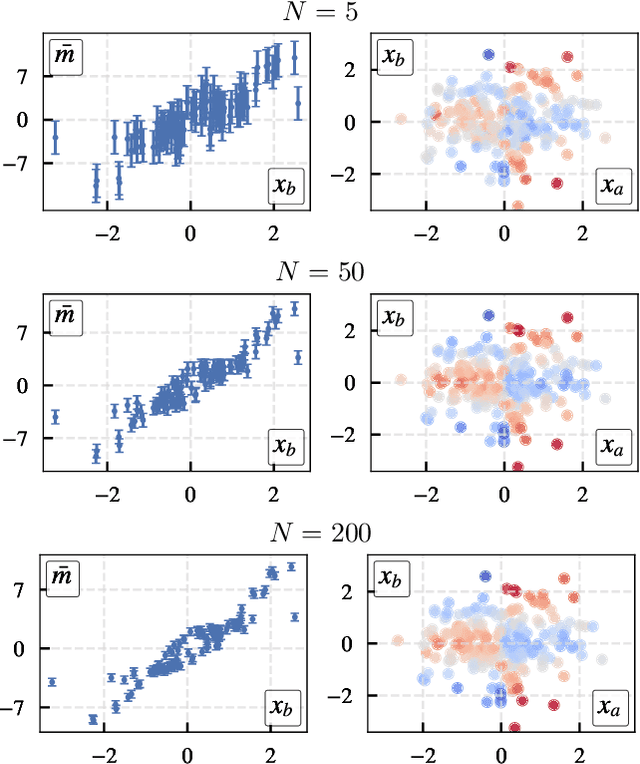
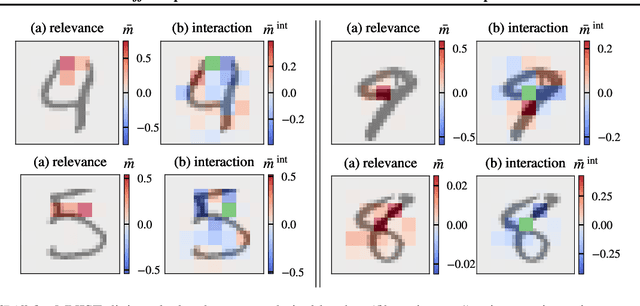
$PredDiff$ is a model-agnostic, local attribution method that is firmly rooted in probability theory. Its simple intuition is to measure prediction changes when marginalizing out feature variables. In this work, we clarify properties of $PredDiff$ and put forward several extensions of the original formalism. Most notably, we introduce a new measure for interaction effects. Interactions are an inevitable step towards a comprehensive understanding of black-box models. Importantly, our framework readily allows to investigate interactions between arbitrary feature subsets and scales linearly with their number. We demonstrate the soundness of $PredDiff$ relevances and interactions both in the classification and regression setting. To this end, we use different analytic, synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge