Enhancing molecular dynamics with equivariant machine-learned densities

Machine-learning interatomic potentials (MLIPs) have enabled molecular dynamics at near ab initio accuracy, yet remain limited to energies and forces by construction, leaving electronic observables such as dipole moments and polarizabilities inaccessible. We introduce DenSNet, a density-first approach to machine-learned electronic structure that learns the Hohenberg--Kohn map from nuclear configurations to the ground-state electron density. Our approach employs an SE(3)-equivariant neural network to predict density coefficients of a flexible atom-centered Gaussian basis, combined with a $Δ$-learning strategy that uses superposed atomic densities as a prior to accelerate training. A second equivariant network then maps the predicted density to the total energy, providing a unified framework for molecular dynamics and electronic structure. We validate DenSNet on ethanol, ethanethiol, and resorcinol, where infrared spectra from machine-learned trajectories show excellent agreement with experimental gas-phase measurements. To test scalability, we train on polythiophene oligomers with 1--6 monomers and extrapolate to chains of up to 12 monomers, generating stable long-time trajectories whose infrared spectra agree with reference density functional theory calculations. Here, we show that reinstating the electron density as the central learned quantity opens a practical route to transferable prediction of spectroscopic and electronic observables in large-scale molecular simulations.

SE(3)-equivariant prediction of molecular wavefunctions and electronic densities

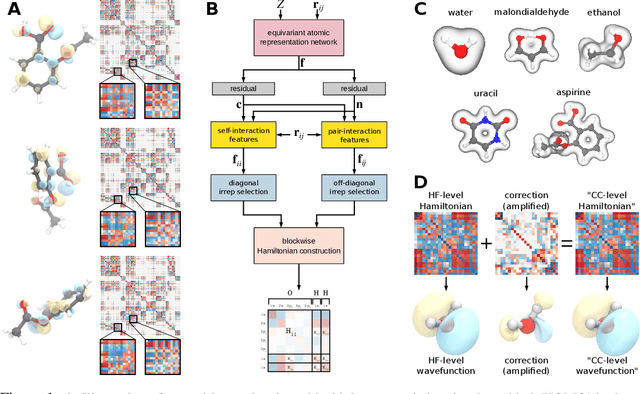
Machine learning has enabled the prediction of quantum chemical properties with high accuracy and efficiency, allowing to bypass computationally costly ab initio calculations. Instead of training on a fixed set of properties, more recent approaches attempt to learn the electronic wavefunction (or density) as a central quantity of atomistic systems, from which all other observables can be derived. This is complicated by the fact that wavefunctions transform non-trivially under molecular rotations, which makes them a challenging prediction target. To solve this issue, we introduce general SE(3)-equivariant operations and building blocks for constructing deep learning architectures for geometric point cloud data and apply them to reconstruct wavefunctions of atomistic systems with unprecedented accuracy. Our model reduces prediction errors by up to two orders of magnitude compared to the previous state-of-the-art and makes it possible to derive properties such as energies and forces directly from the wavefunction in an end-to-end manner. We demonstrate the potential of our approach in a transfer learning application, where a model trained on low accuracy reference wavefunctions implicitly learns to correct for electronic many-body interactions from observables computed at a higher level of theory. Such machine-learned wavefunction surrogates pave the way towards novel semi-empirical methods, offering resolution at an electronic level while drastically decreasing computational cost. While we focus on physics applications in this contribution, the proposed equivariant framework for deep learning on point clouds is promising also beyond, say, in computer vision or graphics.

Learning more expressive joint distributions in multimodal variational methods

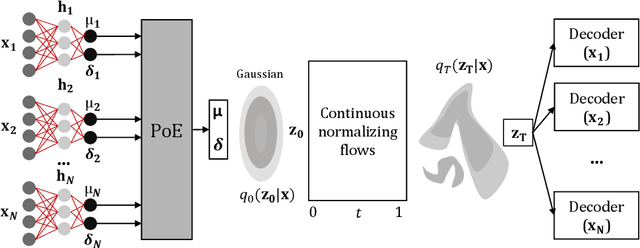
Data often are formed of multiple modalities, which jointly describe the observed phenomena. Modeling the joint distribution of multimodal data requires larger expressive power to capture high-level concepts and provide better data representations. However, multimodal generative models based on variational inference are limited due to the lack of flexibility of the approximate posterior, which is obtained by searching within a known parametric family of distributions. We introduce a method that improves the representational capacity of multimodal variational methods using normalizing flows. It approximates the joint posterior with a simple parametric distribution and subsequently transforms into a more complex one. Through several experiments, we demonstrate that the model improves on state-of-the-art multimodal methods based on variational inference on various computer vision tasks such as colorization, edge and mask detection, and weakly supervised learning. We also show that learning more powerful approximate joint distributions improves the quality of the generated samples. The code of our model is publicly available at https://github.com/SashoNedelkoski/BPFDMVM.

Forecasting Industrial Aging Processes with Machine Learning Methods

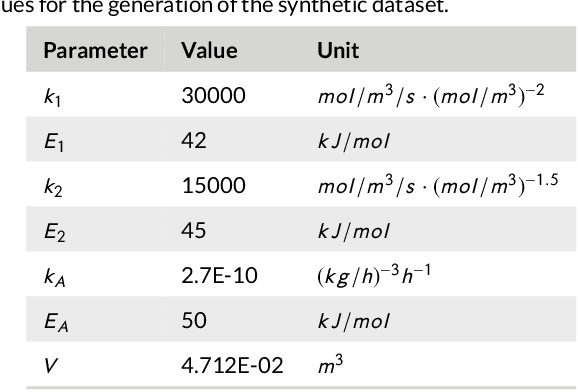
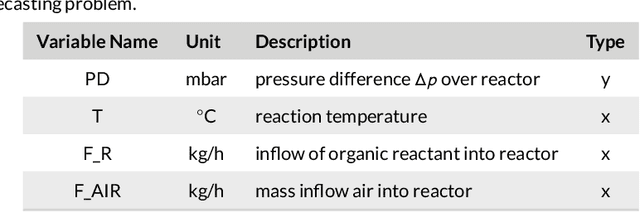
By accurately predicting industrial aging processes (IAPs), it is possible to schedule maintenance events further in advance, thereby ensuring a cost-efficient and reliable operation of the plant. So far, these degradation processes were usually described by mechanistic models or simple empirical prediction models. In this paper, we evaluate a wider range of data-driven models for this task, comparing some traditional stateless models (linear and kernel ridge regression, feed-forward neural networks) to more complex recurrent neural networks (echo state networks and LSTMs). To examine how much historical data is needed to train each of the models, we first examine their performance on a synthetic dataset with known dynamics. Next, the models are tested on real-world data from a large scale chemical plant. Our results show that LSTMs produce near perfect predictions when trained on a large enough dataset, while linear models may generalize better given small datasets with changing conditions.