Flattened one-bit stochastic gradient descent: compressed distributed optimization with controlled variance

We propose a novel algorithm for distributed stochastic gradient descent (SGD) with compressed gradient communication in the parameter-server framework. Our gradient compression technique, named flattened one-bit stochastic gradient descent (FO-SGD), relies on two simple algorithmic ideas: (i) a one-bit quantization procedure leveraging the technique of dithering, and (ii) a randomized fast Walsh-Hadamard transform to flatten the stochastic gradient before quantization. As a result, the approximation of the true gradient in this scheme is biased, but it prevents commonly encountered algorithmic problems, such as exploding variance in the one-bit compression regime, deterioration of performance in the case of sparse gradients, and restrictive assumptions on the distribution of the stochastic gradients. In fact, we show SGD-like convergence guarantees under mild conditions. The compression technique can be used in both directions of worker-server communication, therefore admitting distributed optimization with full communication compression.

The Separation Capacity of Random Neural Networks

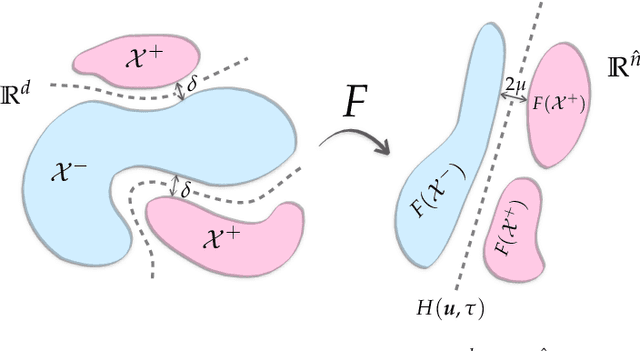
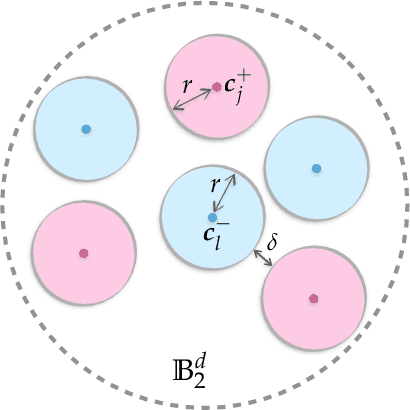
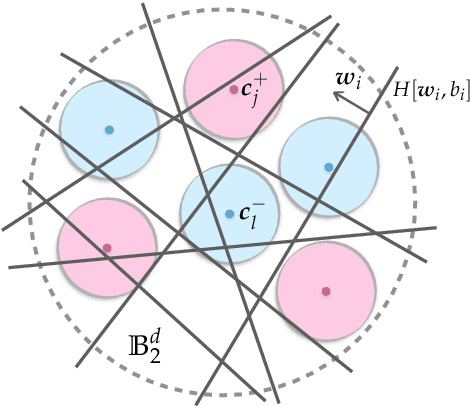
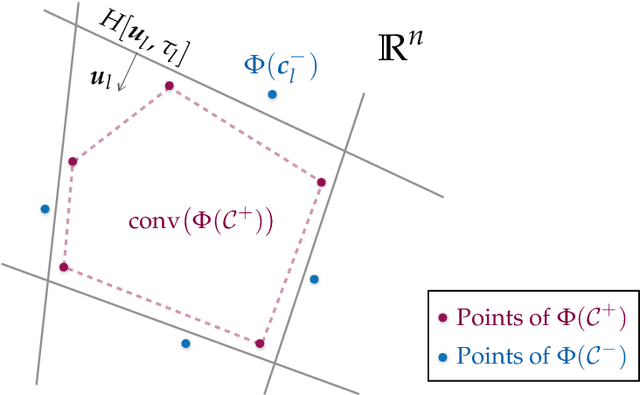
Neural networks with random weights appear in a variety of machine learning applications, most prominently as the initialization of many deep learning algorithms and as a computationally cheap alternative to fully learned neural networks. In the present article we enhance the theoretical understanding of random neural nets by addressing the following data separation problem: under what conditions can a random neural network make two classes $\mathcal{X}^-, \mathcal{X}^+ \subset \mathbb{R}^d$ (with positive distance) linearly separable? We show that a sufficiently large two-layer ReLU-network with standard Gaussian weights and uniformly distributed biases can solve this problem with high probability. Crucially, the number of required neurons is explicitly linked to geometric properties of the underlying sets $\mathcal{X}^-, \mathcal{X}^+$ and their mutual arrangement. This instance-specific viewpoint allows us to overcome the usual curse of dimensionality (exponential width of the layers) in non-pathological situations where the data carries low-complexity structure. We quantify the relevant structure of the data in terms of a novel notion of mutual complexity (based on a localized version of Gaussian mean width), which leads to sound and informative separation guarantees. We connect our result with related lines of work on approximation, memorization, and generalization.