A Mathematical Runtime Analysis of the Non-dominated Sorting Genetic Algorithm III

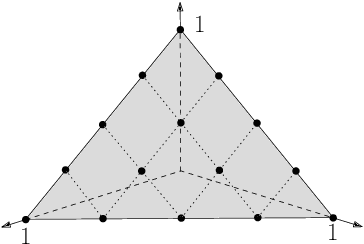
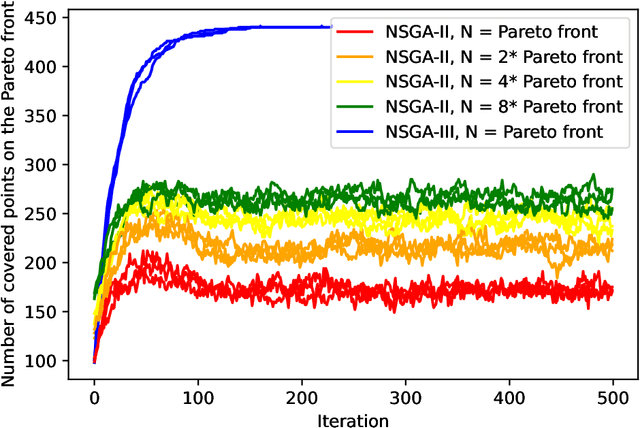
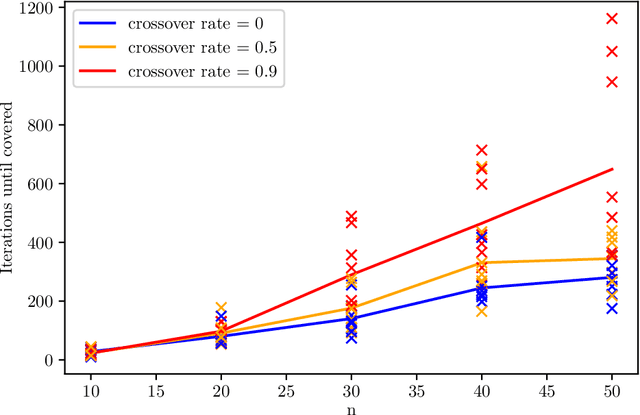
The NSGA-II (Non-dominated Sorting Genetic Algorithm) is the most prominent multi-objective evolutionary algorithm for real-world applications. While it performs evidently well on bi-objective benchmarks, empirical studies suggest that its performance worsens when applied to functions with more than two objectives. As a remedy, the NSGA-III with a slightly adapted selection for the next generation was proposed. In this work, we provide the first mathematical runtime analysis of the NSGA-III, on a 3-objective variant of the \textsc{OneMinMax} benchmark. We prove that employing sufficiently many (at least $\frac{2n^2}{3}+\frac{5n}{\sqrt{3}}+3$) reference points ensures that once a solution for a certain trade-off between the objectives is found, the population contains such a solution in all future iterations. Building on this observation, we show that the expected number of iterations until the population covers the Pareto front is in $O(n^3)$. This result holds for all population sizes that are at least the size of the Pareto front.