Threshold Treewidth and Hypertree Width

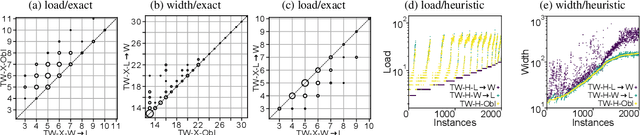
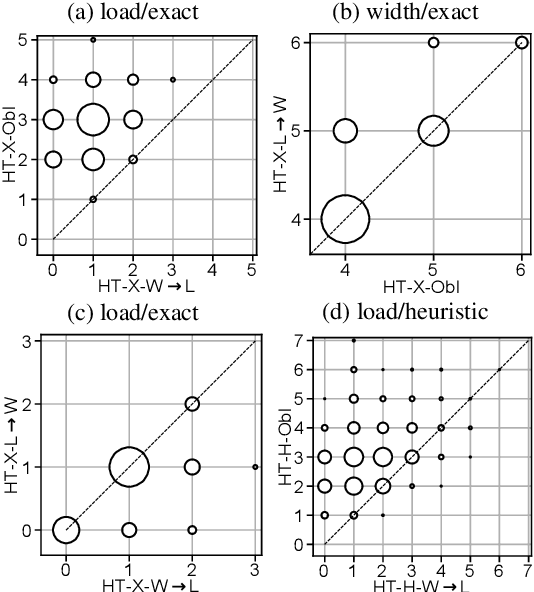
Treewidth and hypertree width have proven to be highly successful structural parameters in the context of the Constraint Satisfaction Problem (CSP). When either of these parameters is bounded by a constant, then CSP becomes solvable in polynomial time. However, here the order of the polynomial in the running time depends on the width, and this is known to be unavoidable; therefore, the problem is not fixed-parameter tractable parameterized by either of these width measures. Here we introduce an enhancement of tree and hypertree width through a novel notion of thresholds, allowing the associated decompositions to take into account information about the computational costs associated with solving the given CSP instance. Aside from introducing these notions, we obtain efficient theoretical as well as empirical algorithms for computing threshold treewidth and hypertree width and show that these parameters give rise to fixed-parameter algorithms for CSP as well as other, more general problems. We complement our theoretical results with experimental evaluations in terms of heuristics as well as exact methods based on SAT/SMT encodings.

Solving the Steiner Tree Problem with few Terminals

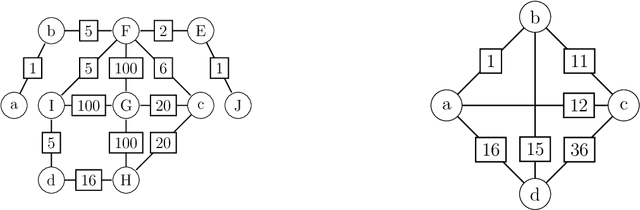
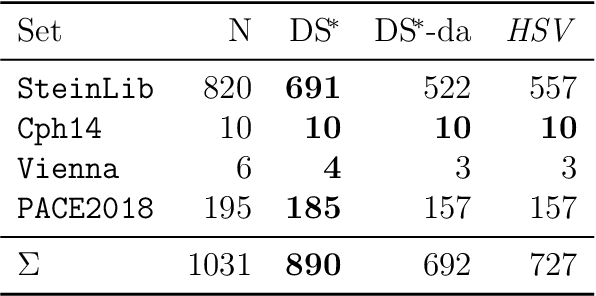
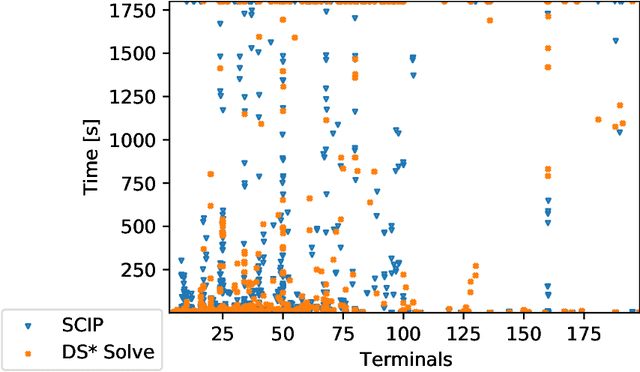
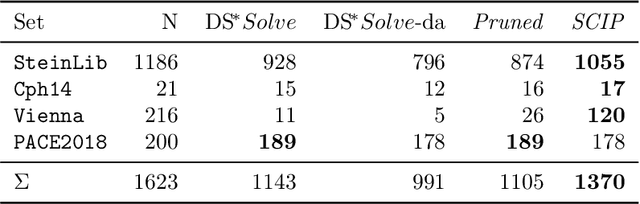
The Steiner tree problem is a well-known problem in network design, routing, and VLSI design. Given a graph, edge costs, and a set of dedicated vertices (terminals), the Steiner tree problem asks to output a sub-graph that connects all terminals at minimum cost. A state-of-the-art algorithm to solve the Steiner tree problem by means of dynamic programming is the Dijkstra-Steiner algorithm. The algorithm builds a Steiner tree of the entire instance by systematically searching for smaller instances, based on subsets of the terminals, and combining Steiner trees for these smaller instances. The search heavily relies on a guiding heuristic function in order to prune the search space. However, to ensure correctness, this algorithm allows only for limited heuristic functions, namely, those that satisfy a so-called consistency condition. In this paper, we enhance the Dijkstra-Steiner algorithm and establish a revisited algorithm, called DS*. The DS* algorithm allows for arbitrary lower bounds as heuristics relaxing the previous condition on the heuristic function. Notably, we can now use linear programming based lower bounds. Further, we capture new requirements for a heuristic function in a condition, which we call admissibility. We show that admissibility is indeed weaker than consistency and establish correctness of the DS* algorithm when using an admissible heuristic function. We implement DS* and combine it with modern preprocessing, resulting in an open-source solver (DS* Solve). Finally, we compare its performance on standard benchmarks and observe a competitive behavior.