Solving the Steiner Tree Problem with few Terminals
Paper and Code
Nov 09, 2020
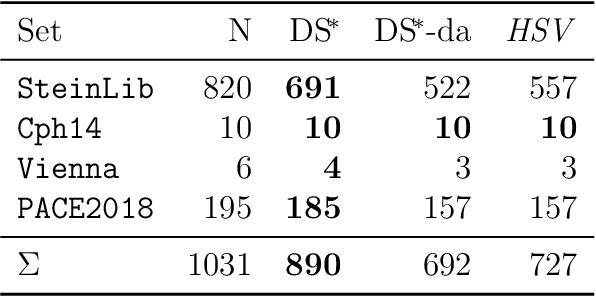
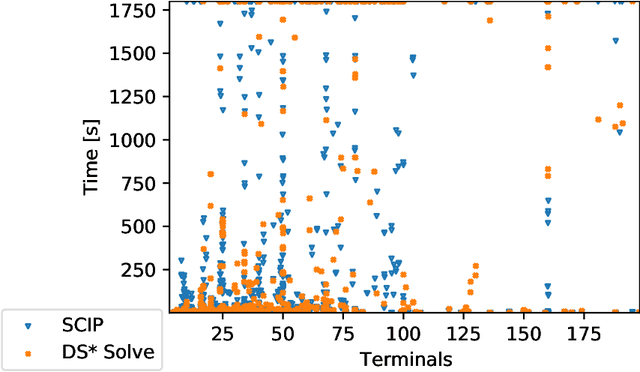
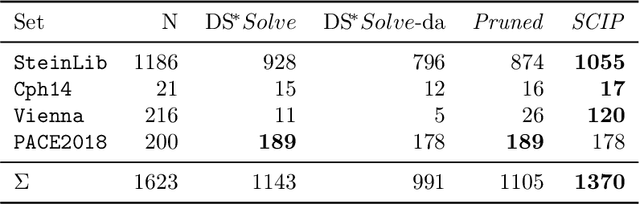
The Steiner tree problem is a well-known problem in network design, routing, and VLSI design. Given a graph, edge costs, and a set of dedicated vertices (terminals), the Steiner tree problem asks to output a sub-graph that connects all terminals at minimum cost. A state-of-the-art algorithm to solve the Steiner tree problem by means of dynamic programming is the Dijkstra-Steiner algorithm. The algorithm builds a Steiner tree of the entire instance by systematically searching for smaller instances, based on subsets of the terminals, and combining Steiner trees for these smaller instances. The search heavily relies on a guiding heuristic function in order to prune the search space. However, to ensure correctness, this algorithm allows only for limited heuristic functions, namely, those that satisfy a so-called consistency condition. In this paper, we enhance the Dijkstra-Steiner algorithm and establish a revisited algorithm, called DS*. The DS* algorithm allows for arbitrary lower bounds as heuristics relaxing the previous condition on the heuristic function. Notably, we can now use linear programming based lower bounds. Further, we capture new requirements for a heuristic function in a condition, which we call admissibility. We show that admissibility is indeed weaker than consistency and establish correctness of the DS* algorithm when using an admissible heuristic function. We implement DS* and combine it with modern preprocessing, resulting in an open-source solver (DS* Solve). Finally, we compare its performance on standard benchmarks and observe a competitive behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge