Improving Decision Trees through the Lens of Parameterized Local Search

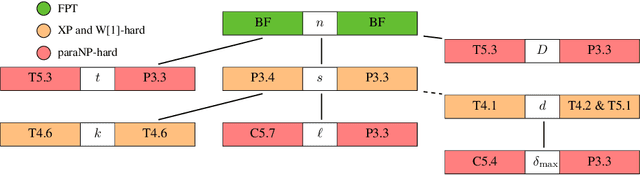
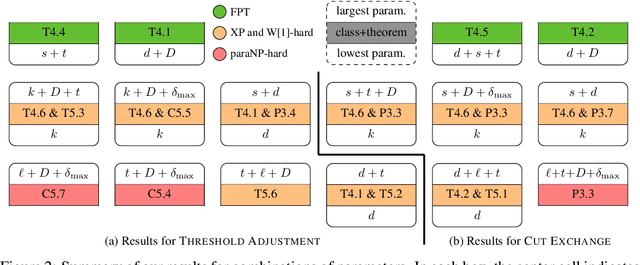
Algorithms for learning decision trees often include heuristic local-search operations such as (1) adjusting the threshold of a cut or (2) also exchanging the feature of that cut. We study minimizing the number of classification errors by performing a fixed number of a single type of these operations. Although we discover that the corresponding problems are NP-complete in general, we provide a comprehensive parameterized-complexity analysis with the aim of determining those properties of the problems that explain the hardness and those that make the problems tractable. For instance, we show that the problems remain hard for a small number $d$ of features or small domain size $D$ but the combination of both yields fixed-parameter tractability. That is, the problems are solvable in $(D + 1)^{2d} \cdot |I|^{O(1)}$ time, where $|I|$ is the size of the input. We also provide a proof-of-concept implementation of this algorithm and report on empirical results.

Optimal Decision Tree Pruning Revisited: Algorithms and Complexity

We present a comprehensive classical and parameterized complexity analysis of decision tree pruning operations, extending recent research on the complexity of learning small decision trees. Thereby, we offer new insights into the computational challenges of decision tree simplification, a crucial aspect of developing interpretable and efficient machine learning models. We focus on fundamental pruning operations of subtree replacement and raising, which are used in heuristics. Surprisingly, while optimal pruning can be performed in polynomial time for subtree replacement, the problem is NP-complete for subtree raising. Therefore, we identify parameters and combinations thereof that lead to fixed-parameter tractability or hardness, establishing a precise borderline between these complexity classes. For example, while subtree raising is hard for small domain size $D$ or number $d$ of features, it can be solved in $D^{2d} \cdot |I|^{O(1)}$ time, where $|I|$ is the input size. We complement our theoretical findings with preliminary experimental results, demonstrating the practical implications of our analysis.

On Computing Optimal Tree Ensembles

Random forests and, more generally, (decision\nobreakdash-)tree ensembles are widely used methods for classification and regression. Recent algorithmic advances allow to compute decision trees that are optimal for various measures such as their size or depth. We are not aware of such research for tree ensembles and aim to contribute to this area. Mainly, we provide two novel algorithms and corresponding lower bounds. First, we are able to carry over and substantially improve on tractability results for decision trees, obtaining a $(6\delta D S)^S \cdot poly$-time algorithm, where $S$ is the number of cuts in the tree ensemble, $D$ the largest domain size, and $\delta$ is the largest number of features in which two examples differ. To achieve this, we introduce the witness-tree technique which also seems promising for practice. Second, we show that dynamic programming, which has been successful for decision trees, may also be viable for tree ensembles, providing an $\ell^n \cdot poly$-time algorithm, where $\ell$ is the number of trees and $n$ the number of examples. Finally, we compare the number of cuts necessary to classify training data sets for decision trees and tree ensembles, showing that ensembles may need exponentially fewer cuts for increasing number of trees.

Threshold Treewidth and Hypertree Width

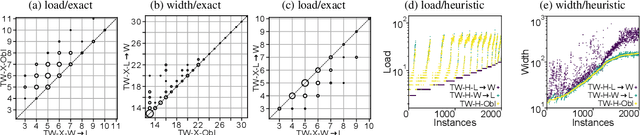
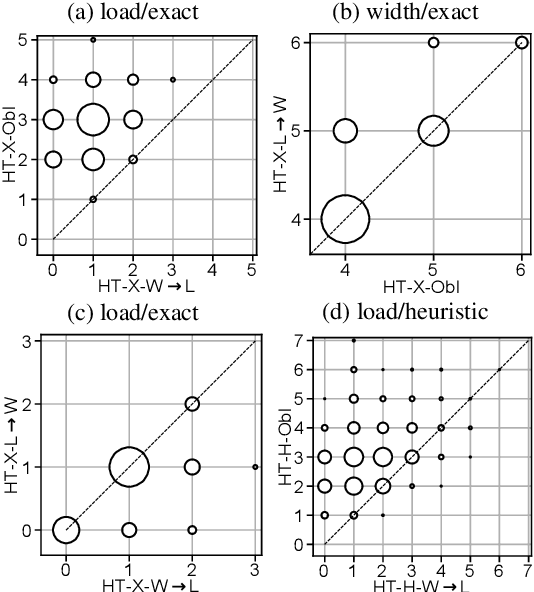
Treewidth and hypertree width have proven to be highly successful structural parameters in the context of the Constraint Satisfaction Problem (CSP). When either of these parameters is bounded by a constant, then CSP becomes solvable in polynomial time. However, here the order of the polynomial in the running time depends on the width, and this is known to be unavoidable; therefore, the problem is not fixed-parameter tractable parameterized by either of these width measures. Here we introduce an enhancement of tree and hypertree width through a novel notion of thresholds, allowing the associated decompositions to take into account information about the computational costs associated with solving the given CSP instance. Aside from introducing these notions, we obtain efficient theoretical as well as empirical algorithms for computing threshold treewidth and hypertree width and show that these parameters give rise to fixed-parameter algorithms for CSP as well as other, more general problems. We complement our theoretical results with experimental evaluations in terms of heuristics as well as exact methods based on SAT/SMT encodings.