Jason Ralph
The Maximum Cover with Rotating Field of View
Sep 27, 2023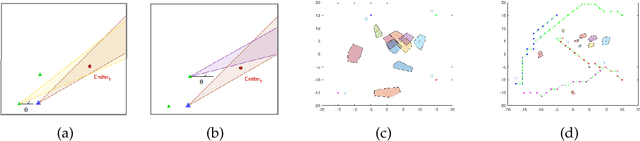
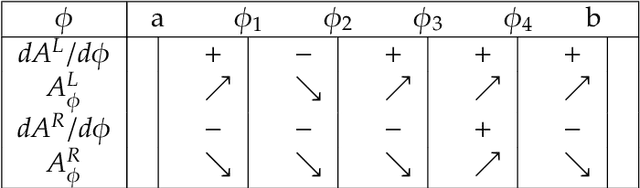
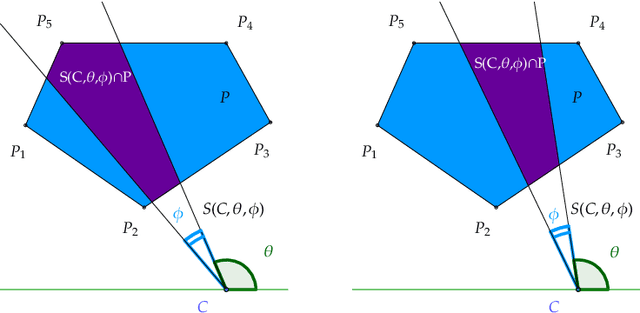
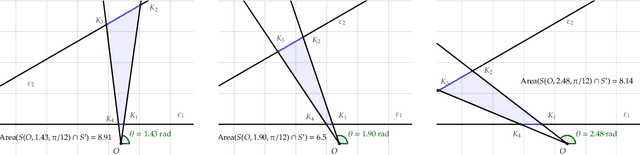
Abstract:Imagine a polygon-shaped platform $P$ and only one static spotlight outside $P$; which direction should the spotlight face to light most of $P$? This problem occurs in maximising the visibility, as well as in limiting the uncertainty in localisation problems. More formally, we define the following maximum cover problem: "Given a convex polygon $P$ and a Field Of View (FOV) with a given centre and inner angle $\phi$; find the direction (an angle of rotation $\theta$) of the FOV such that the intersection between the FOV and $P$ has the maximum area". In this paper, we provide the theoretical foundation for the analysis of the maximum cover with a rotating field of view. The main challenge is that the function of the area $A_{\phi}(\theta)$, with the angle of rotation $\theta$ and the fixed inner angle $\phi$, cannot be approximated directly. We found an alternative way to express it by various compositions of a function $A_{\theta}(\phi)$ (with a restricted inner angle $\phi$ and a fixed direction $\theta$). We show that $A_{\theta}(\phi)$ has an analytical solution in the special case of a two-sector intersection and later provides a constrictive solution for the original problem. Since the optimal solution is a real number, we develop an algorithm that approximates the direction of the field of view, with precision $\varepsilon$, and complexity $\mathcal{O}(n(\log{n}+(\log{\varepsilon})/\phi))$.
Convolutional Neural Networks for Aerial Vehicle Detection and Recognition
Aug 26, 2018



Abstract:This paper investigates the problem of aerial vehicle recognition using a text-guided deep convolutional neural network classifier. The network receives an aerial image and a desired class, and makes a yes or no output by matching the image and the textual description of the desired class. We train and test our model on a synthetic aerial dataset and our desired classes consist of the combination of the class types and colors of the vehicles. This strategy helps when considering more classes in testing than in training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge