Composition and Alignment of Diffusion Models using Constrained Learning

Diffusion models have become prevalent in generative modeling due to their ability to sample from complex distributions. To improve the quality of generated samples and their compliance with user requirements, two commonly used methods are: (i) Alignment, which involves fine-tuning a diffusion model to align it with a reward; and (ii) Composition, which combines several pre-trained diffusion models, each emphasizing a desirable attribute in the generated outputs. However, trade-offs often arise when optimizing for multiple rewards or combining multiple models, as they can often represent competing properties. Existing methods cannot guarantee that the resulting model faithfully generates samples with all the desired properties. To address this gap, we propose a constrained optimization framework that unifies alignment and composition of diffusion models by enforcing that the aligned model satisfies reward constraints and/or remains close to (potentially multiple) pre-trained models. We provide a theoretical characterization of the solutions to the constrained alignment and composition problems and develop a Lagrangian-based primal-dual training algorithm to approximate these solutions. Empirically, we demonstrate the effectiveness and merits of our proposed approach in image generation, applying it to alignment and composition, and show that our aligned or composed model satisfies constraints effectively, and improves on the equally-weighted approach. Our implementation can be found at https://github.com/shervinkhalafi/constrained_comp_align.

Constrained Diffusion Models via Dual Training

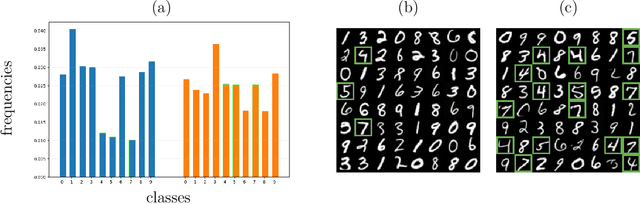
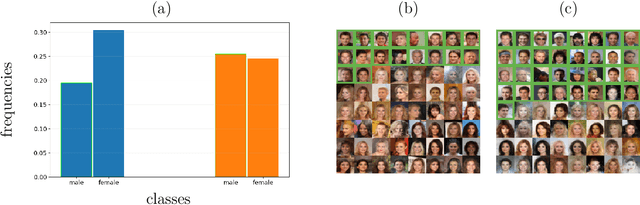
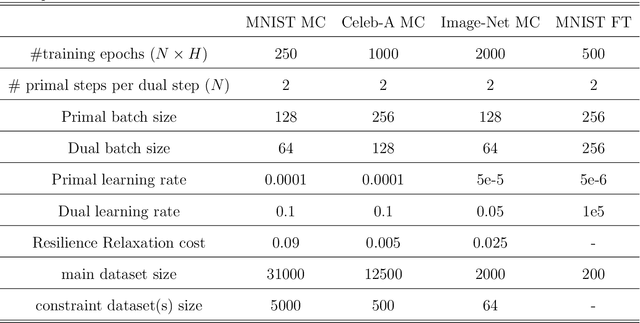
Diffusion models have attained prominence for their ability to synthesize a probability distribution for a given dataset via a diffusion process, enabling the generation of new data points with high fidelity. However, diffusion processes are prone to generating biased data based on the training dataset. To address this issue, we develop constrained diffusion models by imposing diffusion constraints based on desired distributions that are informed by requirements. Specifically, we cast the training of diffusion models under requirements as a constrained distribution optimization problem that aims to reduce the distribution difference between original and generated data while obeying constraints on the distribution of generated data. We show that our constrained diffusion models generate new data from a mixture data distribution that achieves the optimal trade-off among objective and constraints. To train constrained diffusion models, we develop a dual training algorithm and characterize the optimality of the trained constrained diffusion model. We empirically demonstrate the effectiveness of our constrained models in two constrained generation tasks: (i) we consider a dataset with one or more underrepresented classes where we train the model with constraints to ensure fairly sampling from all classes during inference; (ii) we fine-tune a pre-trained diffusion model to sample from a new dataset while avoiding overfitting.

Neural Tangent Kernels Motivate Graph Neural Networks with Cross-Covariance Graphs

Neural tangent kernels (NTKs) provide a theoretical regime to analyze the learning and generalization behavior of over-parametrized neural networks. For a supervised learning task, the association between the eigenvectors of the NTK kernel and given data (a concept referred to as alignment in this paper) can govern the rate of convergence of gradient descent, as well as generalization to unseen data. Building upon this concept, we investigate NTKs and alignment in the context of graph neural networks (GNNs), where our analysis reveals that optimizing alignment translates to optimizing the graph representation or the graph shift operator in a GNN. Our results further establish the theoretical guarantees on the optimality of the alignment for a two-layer GNN and these guarantees are characterized by the graph shift operator being a function of the cross-covariance between the input and the output data. The theoretical insights drawn from the analysis of NTKs are validated by our experiments focused on a multi-variate time series prediction task for a publicly available dataset. Specifically, they demonstrate that GNNs with cross-covariance as the graph shift operator indeed outperform those that operate on the covariance matrix from only the input data.