Towards a Foundation Model for Brain Age Prediction using coVariance Neural Networks

Brain age is the estimate of biological age derived from neuroimaging datasets using machine learning algorithms. Increasing brain age with respect to chronological age can reflect increased vulnerability to neurodegeneration and cognitive decline. In this paper, we study NeuroVNN, based on coVariance neural networks, as a paradigm for foundation model for the brain age prediction application. NeuroVNN is pre-trained as a regression model on healthy population to predict chronological age using cortical thickness features and fine-tuned to estimate brain age in different neurological contexts. Importantly, NeuroVNN adds anatomical interpretability to brain age and has a `scale-free' characteristic that allows its transference to datasets curated according to any arbitrary brain atlas. Our results demonstrate that NeuroVNN can extract biologically plausible brain age estimates in different populations, as well as transfer successfully to datasets of dimensionalities distinct from that for the dataset used to train NeuroVNN.

Neural Tangent Kernels Motivate Graph Neural Networks with Cross-Covariance Graphs

Neural tangent kernels (NTKs) provide a theoretical regime to analyze the learning and generalization behavior of over-parametrized neural networks. For a supervised learning task, the association between the eigenvectors of the NTK kernel and given data (a concept referred to as alignment in this paper) can govern the rate of convergence of gradient descent, as well as generalization to unseen data. Building upon this concept, we investigate NTKs and alignment in the context of graph neural networks (GNNs), where our analysis reveals that optimizing alignment translates to optimizing the graph representation or the graph shift operator in a GNN. Our results further establish the theoretical guarantees on the optimality of the alignment for a two-layer GNN and these guarantees are characterized by the graph shift operator being a function of the cross-covariance between the input and the output data. The theoretical insights drawn from the analysis of NTKs are validated by our experiments focused on a multi-variate time series prediction task for a publicly available dataset. Specifically, they demonstrate that GNNs with cross-covariance as the graph shift operator indeed outperform those that operate on the covariance matrix from only the input data.

Explainable Brain Age Prediction using coVariance Neural Networks

In computational neuroscience, there has been an increased interest in developing machine learning algorithms that leverage brain imaging data to provide estimates of "brain age" for an individual. Importantly, the discordance between brain age and chronological age (referred to as "brain age gap") can capture accelerated aging due to adverse health conditions and therefore, can reflect increased vulnerability towards neurological disease or cognitive impairments. However, widespread adoption of brain age for clinical decision support has been hindered due to lack of transparency and methodological justifications in most existing brain age prediction algorithms. In this paper, we leverage coVariance neural networks (VNN) to propose an anatomically interpretable framework for brain age prediction using cortical thickness features. Specifically, our brain age prediction framework extends beyond the coarse metric of brain age gap in Alzheimer's disease (AD) and we make two important observations: (i) VNNs can assign anatomical interpretability to elevated brain age gap in AD by identifying contributing brain regions, (ii) the interpretability offered by VNNs is contingent on their ability to exploit specific eigenvectors of the anatomical covariance matrix. Together, these observations facilitate an explainable perspective to the task of brain age prediction.

Transferability of coVariance Neural Networks and Application to Interpretable Brain Age Prediction using Anatomical Features

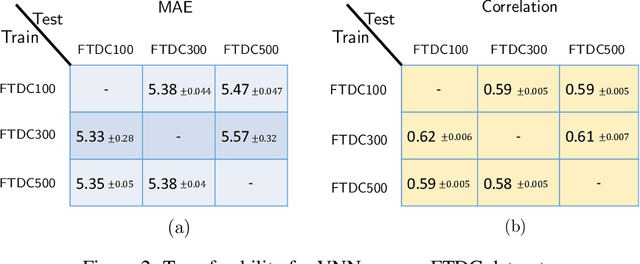
Graph convolutional networks (GCN) leverage topology-driven graph convolutional operations to combine information across the graph for inference tasks. In our recent work, we have studied GCNs with covariance matrices as graphs in the form of coVariance neural networks (VNNs) that draw similarities with traditional PCA-driven data analysis approaches while offering significant advantages over them. In this paper, we first focus on theoretically characterizing the transferability of VNNs. The notion of transferability is motivated from the intuitive expectation that learning models could generalize to "compatible" datasets (possibly of different dimensionalities) with minimal effort. VNNs inherit the scale-free data processing architecture from GCNs and here, we show that VNNs exhibit transferability of performance over datasets whose covariance matrices converge to a limit object. Multi-scale neuroimaging datasets enable the study of the brain at multiple scales and hence, can validate the theoretical results on the transferability of VNNs. To gauge the advantages offered by VNNs in neuroimaging data analysis, we focus on the task of "brain age" prediction using cortical thickness features. In clinical neuroscience, there has been an increased interest in machine learning algorithms which provide estimates of "brain age" that deviate from chronological age. We leverage the architecture of VNNs to extend beyond the coarse metric of brain age gap in Alzheimer's disease (AD) and make two important observations: (i) VNNs can assign anatomical interpretability to elevated brain age gap in AD, and (ii) the interpretability offered by VNNs is contingent on their ability to exploit specific principal components of the anatomical covariance matrix. We further leverage the transferability of VNNs to cross validate the above observations across different datasets.

Predicting Brain Age using Transferable coVariance Neural Networks

The deviation between chronological age and biological age is a well-recognized biomarker associated with cognitive decline and neurodegeneration. Age-related and pathology-driven changes to brain structure are captured by various neuroimaging modalities. These datasets are characterized by high dimensionality as well as collinearity, hence applications of graph neural networks in neuroimaging research routinely use sample covariance matrices as graphs. We have recently studied covariance neural networks (VNNs) that operate on sample covariance matrices using the architecture derived from graph convolutional networks, and we showed VNNs enjoy significant advantages over traditional data analysis approaches. In this paper, we demonstrate the utility of VNNs in inferring brain age using cortical thickness data. Furthermore, our results show that VNNs exhibit multi-scale and multi-site transferability for inferring {brain age}. In the context of brain age in Alzheimer's disease (AD), our experiments show that i) VNN outputs are interpretable as brain age predicted using VNNs is significantly elevated for AD with respect to healthy subjects for different datasets; and ii) VNNs can be transferable, i.e., VNNs trained on one dataset can be transferred to another dataset with different dimensions without retraining for brain age prediction.

coVariance Neural Networks

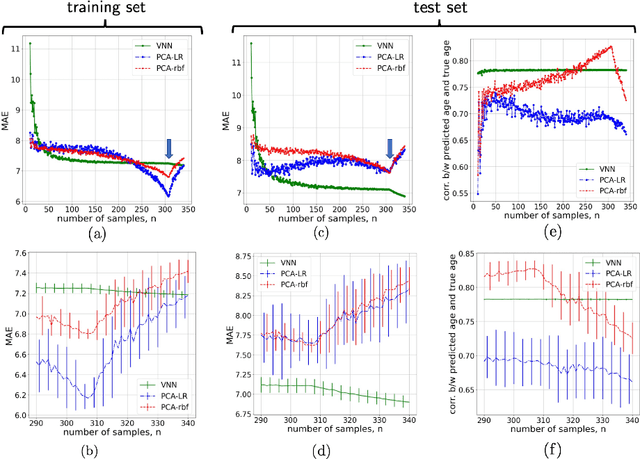
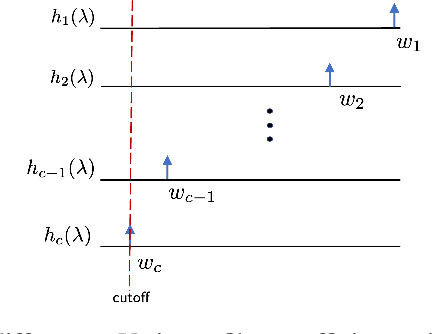
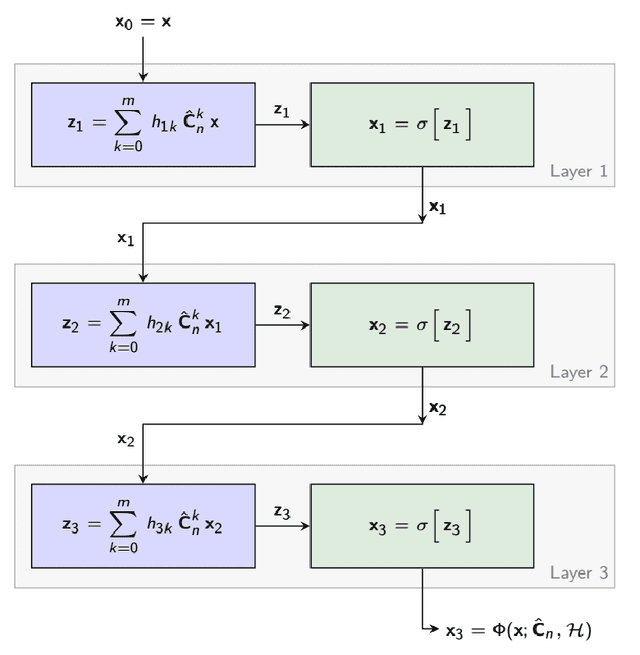
Graph neural networks (GNN) are an effective framework that exploit inter-relationships within graph-structured data for learning. Principal component analysis (PCA) involves the projection of data on the eigenspace of the covariance matrix and draws similarities with the graph convolutional filters in GNNs. Motivated by this observation, we propose a GNN architecture, called coVariance neural network (VNN), that operates on sample covariance matrices as graphs. We theoretically establish the stability of VNNs to perturbations in the covariance matrix, thus, implying an advantage over standard PCA-based data analysis approaches that are prone to instability due to principal components associated with close eigenvalues. Our experiments on real-world datasets validate our theoretical results and show that VNN performance is indeed more stable than PCA-based statistical approaches. Moreover, our experiments on multi-resolution datasets also demonstrate that VNNs are amenable to transferability of performance over covariance matrices of different dimensions; a feature that is infeasible for PCA-based approaches.

Learning Graph Structure from Convolutional Mixtures

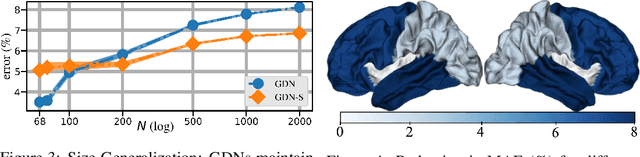
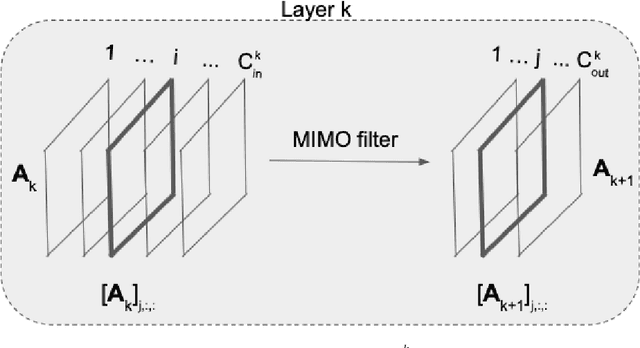
Machine learning frameworks such as graph neural networks typically rely on a given, fixed graph to exploit relational inductive biases and thus effectively learn from network data. However, when said graphs are (partially) unobserved, noisy, or dynamic, the problem of inferring graph structure from data becomes relevant. In this paper, we postulate a graph convolutional relationship between the observed and latent graphs, and formulate the graph learning task as a network inverse (deconvolution) problem. In lieu of eigendecomposition-based spectral methods or iterative optimization solutions, we unroll and truncate proximal gradient iterations to arrive at a parameterized neural network architecture that we call a Graph Deconvolution Network (GDN). GDNs can learn a distribution of graphs in a supervised fashion, perform link prediction or edge-weight regression tasks by adapting the loss function, and they are inherently inductive. We corroborate GDN's superior graph recovery performance and its generalization to larger graphs using synthetic data in supervised settings. Furthermore, we demonstrate the robustness and representation power of GDNs on real world neuroimaging and social network datasets.

Summary Markov Models for Event Sequences

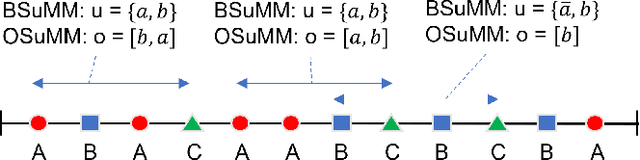
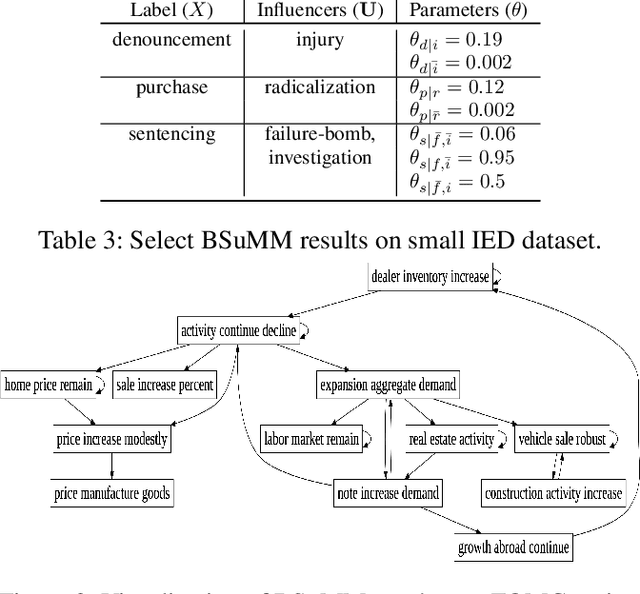
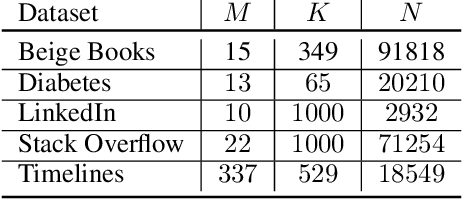
Datasets involving sequences of different types of events without meaningful time stamps are prevalent in many applications, for instance when extracted from textual corpora. We propose a family of models for such event sequences -- summary Markov models -- where the probability of observing an event type depends only on a summary of historical occurrences of its influencing set of event types. This Markov model family is motivated by Granger causal models for time series, with the important distinction that only one event can occur in a position in an event sequence. We show that a unique minimal influencing set exists for any set of event types of interest and choice of summary function, formulate two novel models from the general family that represent specific sequence dynamics, and propose a greedy search algorithm for learning them from event sequence data. We conduct an experimental investigation comparing the proposed models with relevant baselines, and illustrate their knowledge acquisition and discovery capabilities through case studies involving sequences from text.

Faster method for Deep Belief Network based Object classification using DWT

A Deep Belief Network (DBN) requires large, multiple hidden layers with high number of hidden units to learn good features from the raw pixels of large images. This implies more training time as well as computational complexity. By integrating DBN with Discrete Wavelet Transform (DWT), both training time and computational complexity can be reduced. The low resolution images obtained after application of DWT are used to train multiple DBNs. The results obtained from these DBNs are combined using a weighted voting algorithm. The performance of this method is found to be competent and faster in comparison with that of traditional DBNs.