Donghwan Lee
Adaptive Policy Backbone via Shared Network
Sep 26, 2025Abstract:Reinforcement learning (RL) has achieved impressive results across domains, yet learning an optimal policy typically requires extensive interaction data, limiting practical deployment. A common remedy is to leverage priors, such as pre-collected datasets or reference policies, but their utility degrades under task mismatch between training and deployment. While prior work has sought to address this mismatch, it has largely been restricted to in-distribution settings. To address this challenge, we propose Adaptive Policy Backbone (APB), a meta-transfer RL method that inserts lightweight linear layers before and after a shared backbone, thereby enabling parameter-efficient fine-tuning (PEFT) while preserving prior knowledge during adaptation. Our results show that APB improves sample efficiency over standard RL and adapts to out-of-distribution (OOD) tasks where existing meta-RL baselines typically fail.
Pretraining a Shared Q-Network for Data-Efficient Offline Reinforcement Learning
May 09, 2025Abstract:Offline reinforcement learning (RL) aims to learn a policy from a static dataset without further interactions with the environment. Collecting sufficiently large datasets for offline RL is exhausting since this data collection requires colossus interactions with environments and becomes tricky when the interaction with the environment is restricted. Hence, how an agent learns the best policy with a minimal static dataset is a crucial issue in offline RL, similar to the sample efficiency problem in online RL. In this paper, we propose a simple yet effective plug-and-play pretraining method to initialize a feature of a $Q$-network to enhance data efficiency in offline RL. Specifically, we introduce a shared $Q$-network structure that outputs predictions of the next state and $Q$-value. We pretrain the shared $Q$-network through a supervised regression task that predicts a next state and trains the shared $Q$-network using diverse offline RL methods. Through extensive experiments, we empirically demonstrate that our method enhances the performance of existing popular offline RL methods on the D4RL, Robomimic and V-D4RL benchmarks. Furthermore, we show that our method significantly boosts data-efficient offline RL across various data qualities and data distributions trough D4RL and ExoRL benchmarks. Notably, our method adapted with only 10% of the dataset outperforms standard algorithms even with full datasets.
Understanding the theoretical properties of projected Bellman equation, linear Q-learning, and approximate value iteration
Apr 15, 2025
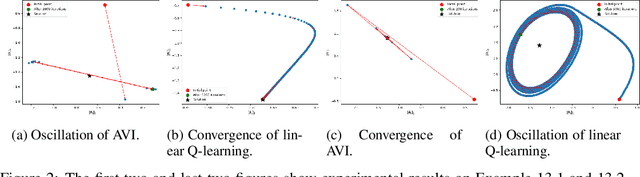


Abstract:In this paper, we study the theoretical properties of the projected Bellman equation (PBE) and two algorithms to solve this equation: linear Q-learning and approximate value iteration (AVI). We consider two sufficient conditions for the existence of a solution to PBE : strictly negatively row dominating diagonal (SNRDD) assumption and a condition motivated by the convergence of AVI. The SNRDD assumption also ensures the convergence of linear Q-learning, and its relationship with the convergence of AVI is examined. Lastly, several interesting observations on the solution of PBE are provided when using $\epsilon$-greedy policy.
Deep Q-Learning with Gradient Target Tracking
Mar 20, 2025Abstract:This paper introduces Q-learning with gradient target tracking, a novel reinforcement learning framework that provides a learned continuous target update mechanism as an alternative to the conventional hard update paradigm. In the standard deep Q-network (DQN), the target network is a copy of the online network's weights, held fixed for a number of iterations before being periodically replaced via a hard update. While this stabilizes training by providing consistent targets, it introduces a new challenge: the hard update period must be carefully tuned to achieve optimal performance. To address this issue, we propose two gradient-based target update methods: DQN with asymmetric gradient target tracking (AGT2-DQN) and DQN with symmetric gradient target tracking (SGT2-DQN). These methods replace the conventional hard target updates with continuous and structured updates using gradient descent, which effectively eliminates the need for manual tuning. We provide a theoretical analysis proving the convergence of these methods in tabular settings. Additionally, empirical evaluations demonstrate their advantages over standard DQN baselines, which suggest that gradient-based target updates can serve as an effective alternative to conventional target update mechanisms in Q-learning.
OFF-CLIP: Improving Normal Detection Confidence in Radiology CLIP with Simple Off-Diagonal Term Auto-Adjustment
Mar 03, 2025



Abstract:Contrastive Language-Image Pre-Training (CLIP) has enabled zero-shot classification in radiology, reducing reliance on manual annotations. However, conventional contrastive learning struggles with normal case detection due to its strict intra-sample alignment, which disrupts normal sample clustering and leads to high false positives (FPs) and false negatives (FNs). To address these issues, we propose OFF-CLIP, a contrastive learning refinement that improves normal detection by introducing an off-diagonal term loss to enhance normal sample clustering and applying sentence-level text filtering to mitigate FNs by removing misaligned normal statements from abnormal reports. OFF-CLIP can be applied to radiology CLIP models without requiring any architectural modifications. Experimental results show that OFF-CLIP significantly improves normal classification, achieving a 0.61 Area under the curve (AUC) increase on VinDr-CXR over CARZero, the state-of-the-art zero-shot classification baseline, while maintaining or improving abnormal classification performance. Additionally, OFF-CLIP enhances zero-shot grounding by improving pointing game accuracy, confirming better anomaly localization. These results demonstrate OFF-CLIP's effectiveness as a robust and efficient enhancement for medical vision-language models.
Robust Deterministic Policy Gradient for Disturbance Attenuation and Its Application to Quadrotor Control
Feb 28, 2025



Abstract:Practical control systems pose significant challenges in identifying optimal control policies due to uncertainties in the system model and external disturbances. While $H_\infty$ control techniques are commonly used to design robust controllers that mitigate the effects of disturbances, these methods often require complex and computationally intensive calculations. To address this issue, this paper proposes a reinforcement learning algorithm called Robust Deterministic Policy Gradient (RDPG), which formulates the $H_\infty$ control problem as a two-player zero-sum dynamic game. In this formulation, one player (the user) aims to minimize the cost, while the other player (the adversary) seeks to maximize it. We then employ deterministic policy gradient (DPG) and its deep reinforcement learning counterpart to train a robust control policy with effective disturbance attenuation. In particular, for practical implementation, we introduce an algorithm called robust deep deterministic policy gradient (RDDPG), which employs a deep neural network architecture and integrates techniques from the twin-delayed deep deterministic policy gradient (TD3) to enhance stability and learning efficiency. To evaluate the proposed algorithm, we implement it on an unmanned aerial vehicle (UAV) tasked with following a predefined path in a disturbance-prone environment. The experimental results demonstrate that the proposed method outperforms other control approaches in terms of robustness against disturbances, enabling precise real-time tracking of moving targets even under severe disturbance conditions.
Analysis of Off-Policy $n$-Step TD-Learning with Linear Function Approximation
Feb 13, 2025
Abstract:This paper analyzes multi-step temporal difference (TD)-learning algorithms within the ``deadly triad'' scenario, characterized by linear function approximation, off-policy learning, and bootstrapping. In particular, we prove that $n$-step TD-learning algorithms converge to a solution as the sampling horizon $n$ increases sufficiently. The paper is divided into two parts. In the first part, we comprehensively examine the fundamental properties of their model-based deterministic counterparts, including projected value iteration, gradient descent algorithms, which can be viewed as prototype deterministic algorithms whose analysis plays a pivotal role in understanding and developing their model-free reinforcement learning counterparts. In particular, we prove that these algorithms converge to meaningful solutions when $n$ is sufficiently large. Based on these findings, in the second part, two $n$-step TD-learning algorithms are proposed and analyzed, which can be seen as the model-free reinforcement learning counterparts of the model-based deterministic algorithms.
Finite-Time Analysis of Simultaneous Double Q-learning
Jun 14, 2024Abstract:$Q$-learning is one of the most fundamental reinforcement learning (RL) algorithms. Despite its widespread success in various applications, it is prone to overestimation bias in the $Q$-learning update. To address this issue, double $Q$-learning employs two independent $Q$-estimators which are randomly selected and updated during the learning process. This paper proposes a modified double $Q$-learning, called simultaneous double $Q$-learning (SDQ), with its finite-time analysis. SDQ eliminates the need for random selection between the two $Q$-estimators, and this modification allows us to analyze double $Q$-learning through the lens of a novel switching system framework facilitating efficient finite-time analysis. Empirical studies demonstrate that SDQ converges faster than double $Q$-learning while retaining the ability to mitigate the maximization bias. Finally, we derive a finite-time expected error bound for SDQ.
A finite time analysis of distributed Q-learning
May 23, 2024Abstract:Multi-agent reinforcement learning (MARL) has witnessed a remarkable surge in interest, fueled by the empirical success achieved in applications of single-agent reinforcement learning (RL). In this study, we consider a distributed Q-learning scenario, wherein a number of agents cooperatively solve a sequential decision making problem without access to the central reward function which is an average of the local rewards. In particular, we study finite-time analysis of a distributed Q-learning algorithm, and provide a new sample complexity result of $\tilde{\mathcal{O}}\left( \min\left\{\frac{1}{\epsilon^2}\frac{t_{\text{mix}}}{(1-\gamma)^6 d_{\min}^4 } ,\frac{1}{\epsilon}\frac{\sqrt{|\gS||\gA|}}{(1-\sigma_2(\boldsymbol{W}))(1-\gamma)^4 d_{\min}^3} \right\}\right)$ under tabular lookup
Unified ODE Analysis of Smooth Q-Learning Algorithms
Apr 24, 2024Abstract:Convergence of Q-learning has been the focus of extensive research over the past several decades. Recently, an asymptotic convergence analysis for Q-learning was introduced using a switching system framework. This approach applies the so-called ordinary differential equation (ODE) approach to prove the convergence of the asynchronous Q-learning modeled as a continuous-time switching system, where notions from switching system theory are used to prove its asymptotic stability without using explicit Lyapunov arguments. However, to prove stability, restrictive conditions, such as quasi-monotonicity, must be satisfied for the underlying switching systems, which makes it hard to easily generalize the analysis method to other reinforcement learning algorithms, such as the smooth Q-learning variants. In this paper, we present a more general and unified convergence analysis that improves upon the switching system approach and can analyze Q-learning and its smooth variants. The proposed analysis is motivated by previous work on the convergence of synchronous Q-learning based on $p$-norm serving as a Lyapunov function. However, the proposed analysis addresses more general ODE models that can cover both asynchronous Q-learning and its smooth versions with simpler frameworks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge