Understanding the theoretical properties of projected Bellman equation, linear Q-learning, and approximate value iteration

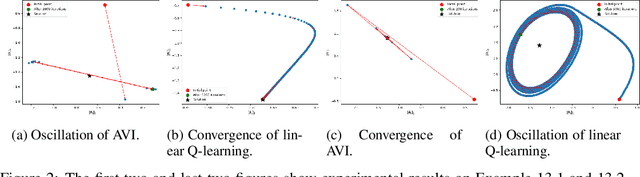
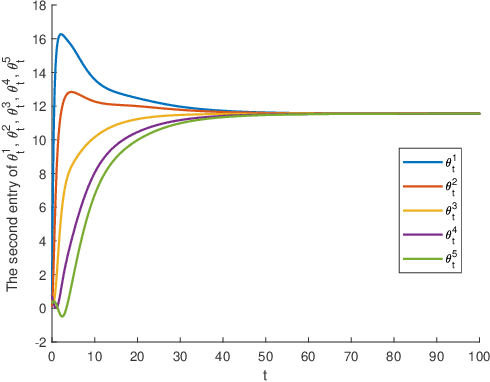
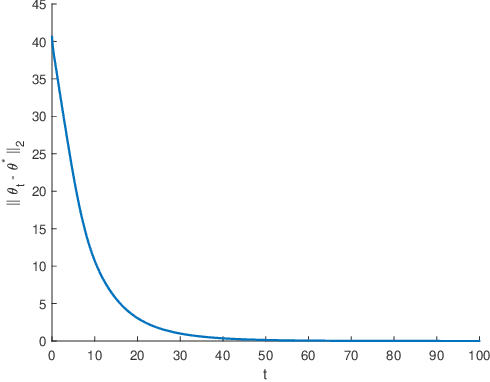
In this paper, we study the theoretical properties of the projected Bellman equation (PBE) and two algorithms to solve this equation: linear Q-learning and approximate value iteration (AVI). We consider two sufficient conditions for the existence of a solution to PBE : strictly negatively row dominating diagonal (SNRDD) assumption and a condition motivated by the convergence of AVI. The SNRDD assumption also ensures the convergence of linear Q-learning, and its relationship with the convergence of AVI is examined. Lastly, several interesting observations on the solution of PBE are provided when using $\epsilon$-greedy policy.

Analysis of Off-Policy $n$-Step TD-Learning with Linear Function Approximation

This paper analyzes multi-step temporal difference (TD)-learning algorithms within the ``deadly triad'' scenario, characterized by linear function approximation, off-policy learning, and bootstrapping. In particular, we prove that $n$-step TD-learning algorithms converge to a solution as the sampling horizon $n$ increases sufficiently. The paper is divided into two parts. In the first part, we comprehensively examine the fundamental properties of their model-based deterministic counterparts, including projected value iteration, gradient descent algorithms, which can be viewed as prototype deterministic algorithms whose analysis plays a pivotal role in understanding and developing their model-free reinforcement learning counterparts. In particular, we prove that these algorithms converge to meaningful solutions when $n$ is sufficiently large. Based on these findings, in the second part, two $n$-step TD-learning algorithms are proposed and analyzed, which can be seen as the model-free reinforcement learning counterparts of the model-based deterministic algorithms.

A finite time analysis of distributed Q-learning

Multi-agent reinforcement learning (MARL) has witnessed a remarkable surge in interest, fueled by the empirical success achieved in applications of single-agent reinforcement learning (RL). In this study, we consider a distributed Q-learning scenario, wherein a number of agents cooperatively solve a sequential decision making problem without access to the central reward function which is an average of the local rewards. In particular, we study finite-time analysis of a distributed Q-learning algorithm, and provide a new sample complexity result of $\tilde{\mathcal{O}}\left( \min\left\{\frac{1}{\epsilon^2}\frac{t_{\text{mix}}}{(1-\gamma)^6 d_{\min}^4 } ,\frac{1}{\epsilon}\frac{\sqrt{|\gS||\gA|}}{(1-\sigma_2(\boldsymbol{W}))(1-\gamma)^4 d_{\min}^3} \right\}\right)$ under tabular lookup

Finite-Time Error Analysis of Online Model-Based Q-Learning with a Relaxed Sampling Model

Reinforcement learning has witnessed significant advancements, particularly with the emergence of model-based approaches. Among these, $Q$-learning has proven to be a powerful algorithm in model-free settings. However, the extension of $Q$-learning to a model-based framework remains relatively unexplored. In this paper, we delve into the sample complexity of $Q$-learning when integrated with a model-based approach. Through theoretical analyses and empirical evaluations, we seek to elucidate the conditions under which model-based $Q$-learning excels in terms of sample efficiency compared to its model-free counterpart.

A primal-dual perspective for distributed TD-learning

The goal of this paper is to investigate distributed temporal difference (TD) learning for a networked multi-agent Markov decision process. The proposed approach is based on distributed optimization algorithms, which can be interpreted as primal-dual Ordinary differential equation (ODE) dynamics subject to null-space constraints. Based on the exponential convergence behavior of the primal-dual ODE dynamics subject to null-space constraints, we examine the behavior of the final iterate in various distributed TD-learning scenarios, considering both constant and diminishing step-sizes and incorporating both i.i.d. and Markovian observation models. Unlike existing methods, the proposed algorithm does not require the assumption that the underlying communication network structure is characterized by a doubly stochastic matrix.

An O.D.E. Framework of Distributed TD-Learning for Networked Multi-Agent Markov Decision Processes

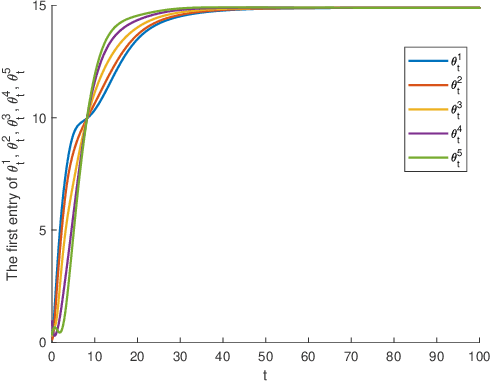
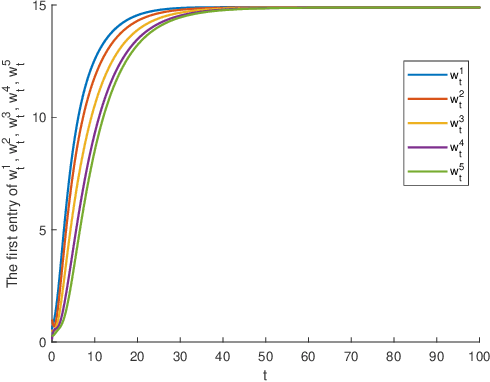
The primary objective of this paper is to investigate distributed ordinary differential equation (ODE) and distributed temporal difference (TD) learning algorithms for networked multi-agent Markov decision problems (MAMDPs). In our study, we adopt a distributed multi-agent framework where individual agents have access only to their own rewards, lacking insights into the rewards of other agents. Additionally, each agent has the ability to share its parameters with neighboring agents through a communication network, represented by a graph. Our contributions can be summarized in two key points: 1) We introduce novel distributed ODEs, inspired by the averaging consensus method in the continuous-time domain. The convergence of the ODEs is assessed through control theory perspectives. 2) Building upon the aforementioned ODEs, we devise new distributed TD-learning algorithms. A standout feature of one of our proposed distributed ODEs is its incorporation of two independent dynamic systems, each with a distinct role. This characteristic sets the stage for a novel distributed TD-learning strategy, the convergence of which can potentially be established using Borkar-Meyn theorem.

Temporal Difference Learning with Experience Replay

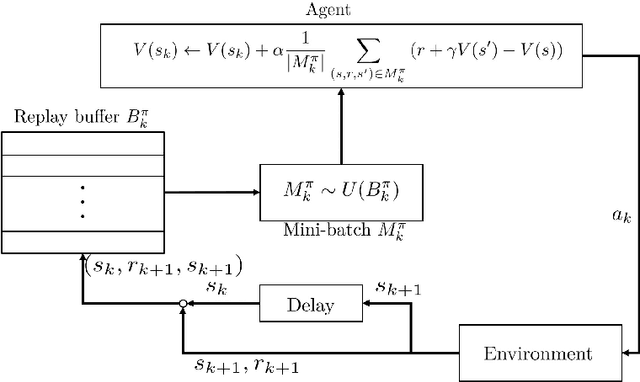
Temporal-difference (TD) learning is widely regarded as one of the most popular algorithms in reinforcement learning (RL). Despite its widespread use, it has only been recently that researchers have begun to actively study its finite time behavior, including the finite time bound on mean squared error and sample complexity. On the empirical side, experience replay has been a key ingredient in the success of deep RL algorithms, but its theoretical effects on RL have yet to be fully understood. In this paper, we present a simple decomposition of the Markovian noise terms and provide finite-time error bounds for TD-learning with experience replay. Specifically, under the Markovian observation model, we demonstrate that for both the averaged iterate and final iterate cases, the error term induced by a constant step-size can be effectively controlled by the size of the replay buffer and the mini-batch sampled from the experience replay buffer.

Backstepping Temporal Difference Learning

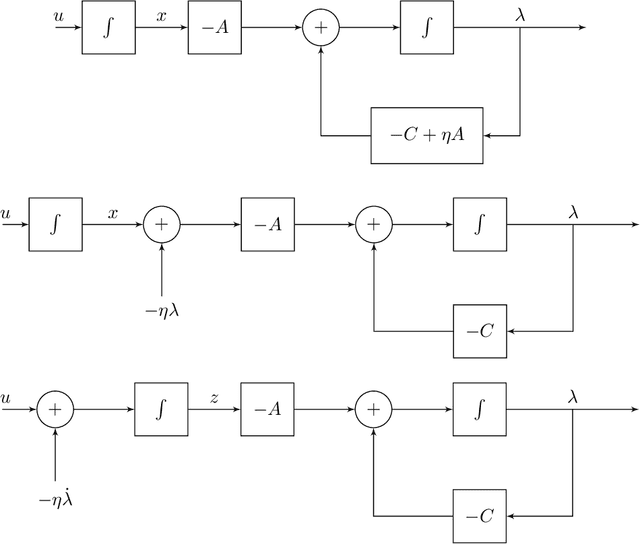
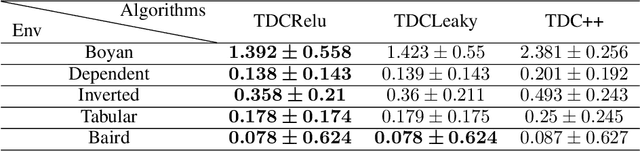
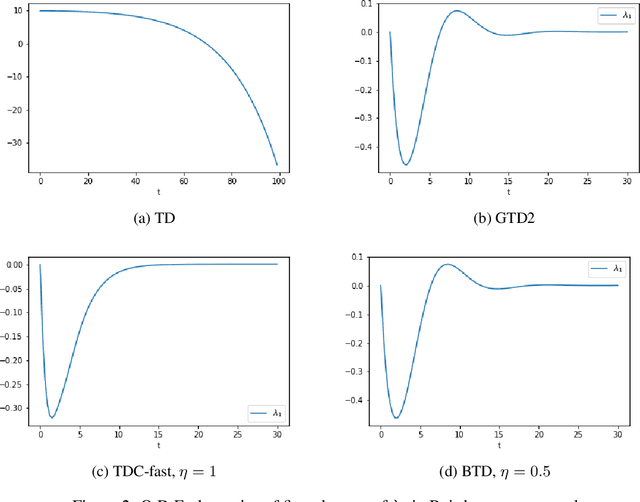
Off-policy learning ability is an important feature of reinforcement learning (RL) for practical applications. However, even one of the most elementary RL algorithms, temporal-difference (TD) learning, is known to suffer form divergence issue when the off-policy scheme is used together with linear function approximation. To overcome the divergent behavior, several off-policy TD-learning algorithms, including gradient-TD learning (GTD), and TD-learning with correction (TDC), have been developed until now. In this work, we provide a unified view of such algorithms from a purely control-theoretic perspective, and propose a new convergent algorithm. Our method relies on the backstepping technique, which is widely used in nonlinear control theory. Finally, convergence of the proposed algorithm is experimentally verified in environments where the standard TD-learning is known to be unstable.

Finite-Time Analysis of Asynchronous Q-learning under Diminishing Step-Size from Control-Theoretic View

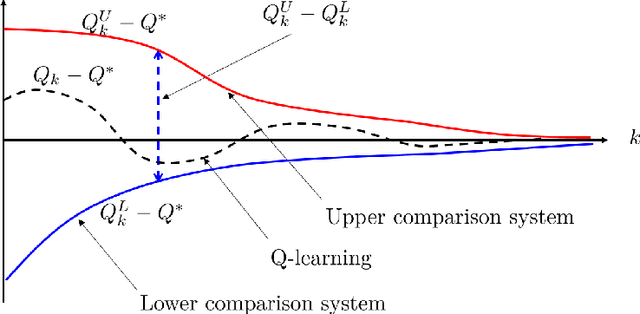
Q-learning has long been one of the most popular reinforcement learning algorithms, and theoretical analysis of Q-learning has been an active research topic for decades. Although researches on asymptotic convergence analysis of Q-learning have a long tradition, non-asymptotic convergence has only recently come under active study. The main goal of this paper is to investigate new finite-time analysis of asynchronous Q-learning under Markovian observation models via a control system viewpoint. In particular, we introduce a discrete-time time-varying switching system model of Q-learning with diminishing step-sizes for our analysis, which significantly improves recent development of the switching system analysis with constant step-sizes, and leads to \(\mathcal{O}\left( \sqrt{\frac{\log k}{k}} \right)\) convergence rate that is comparable to or better than most of the state of the art results in the literature. In the mean while, a technique using the similarly transformation is newly applied to avoid the difficulty in the analysis posed by diminishing step-sizes. The proposed analysis brings in additional insights, covers different scenarios, and provides new simplified templates for analysis to deepen our understanding on Q-learning via its unique connection to discrete-time switching systems.

Regularized Q-learning

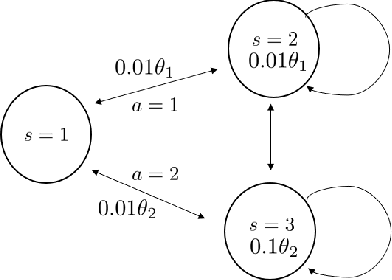
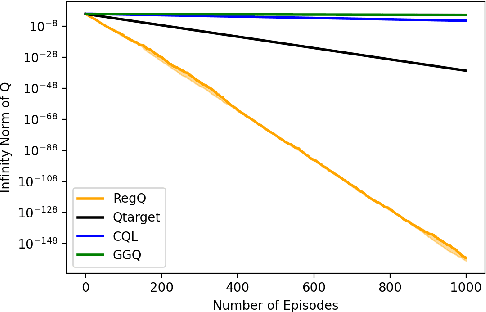
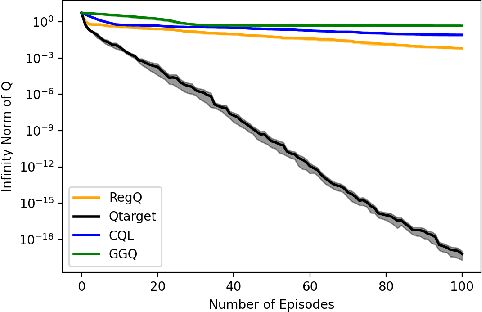
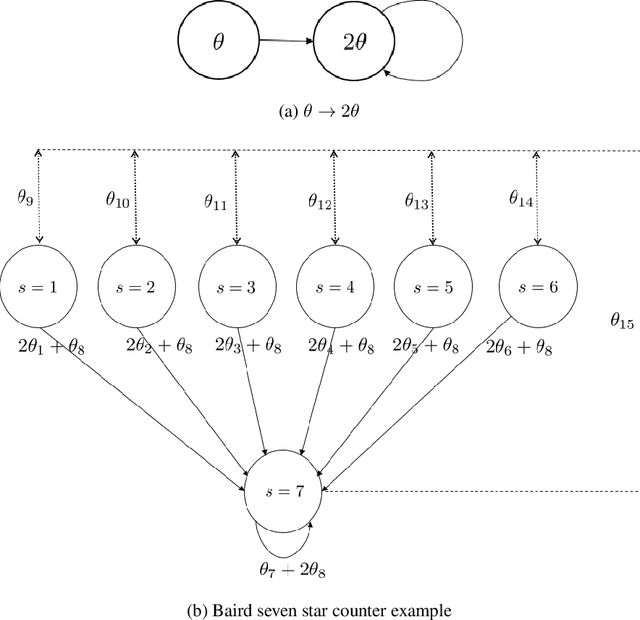
Q-learning is widely used algorithm in reinforcement learning community. Under the lookup table setting, its convergence is well established. However, its behavior is known to be unstable with the linear function approximation case. This paper develops a new Q-learning algorithm that converges when linear function approximation is used. We prove that simply adding an appropriate regularization term ensures convergence of the algorithm. We prove its stability using a recent analysis tool based on switching system models. Moreover, we experimentally show that it converges in environments where Q-learning with linear function approximation has known to diverge. We also provide an error bound on the solution where the algorithm converges.