On the Local Quadratic Stability of T-S Fuzzy Systems in the Vicinity of the Origin

The main goal of this paper is to introduce new local stability conditions for continuous-time Takagi-Sugeno (T-S) fuzzy systems. These stability conditions are based on linear matrix inequalities (LMIs) in combination with quadratic Lyapunov functions. Moreover, they integrate information on the membership functions at the origin and effectively leverage the linear structure of the underlying nonlinear system in the vicinity of the origin. As a result, the proposed conditions are proved to be less conservative compared to existing methods using fuzzy Lyapunov functions in the literature. Moreover, we establish that the proposed methods offer necessary and sufficient conditions for the local exponential stability of T-S fuzzy systems. The paper also includes discussions on the inherent limitations associated with fuzzy Lyapunov approaches. To demonstrate the theoretical results, we provide comprehensive examples that elucidate the core concepts and validate the efficacy of the proposed conditions.

An O.D.E. Framework of Distributed TD-Learning for Networked Multi-Agent Markov Decision Processes

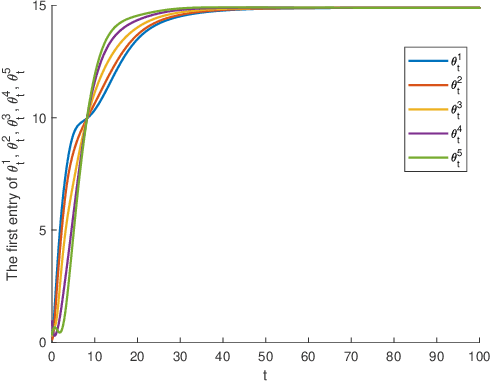
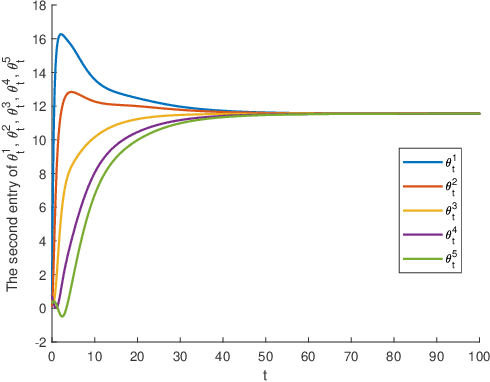
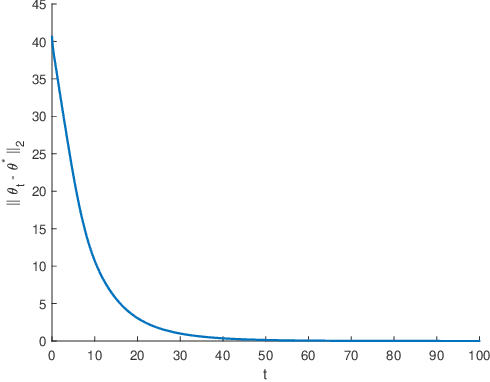
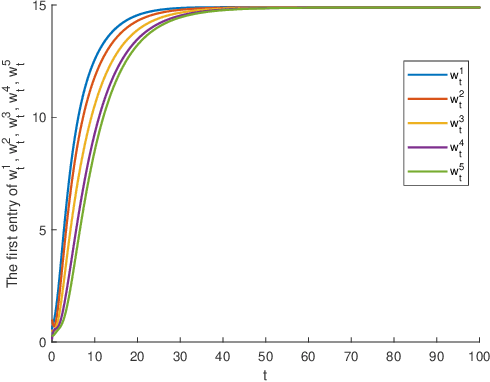
The primary objective of this paper is to investigate distributed ordinary differential equation (ODE) and distributed temporal difference (TD) learning algorithms for networked multi-agent Markov decision problems (MAMDPs). In our study, we adopt a distributed multi-agent framework where individual agents have access only to their own rewards, lacking insights into the rewards of other agents. Additionally, each agent has the ability to share its parameters with neighboring agents through a communication network, represented by a graph. Our contributions can be summarized in two key points: 1) We introduce novel distributed ODEs, inspired by the averaging consensus method in the continuous-time domain. The convergence of the ODEs is assessed through control theory perspectives. 2) Building upon the aforementioned ODEs, we devise new distributed TD-learning algorithms. A standout feature of one of our proposed distributed ODEs is its incorporation of two independent dynamic systems, each with a distinct role. This characteristic sets the stage for a novel distributed TD-learning strategy, the convergence of which can potentially be established using Borkar-Meyn theorem.

Analysis of Temporal Difference Learning: Linear System Approach

The goal of this technical note is to introduce a new finite-time convergence analysis of temporal difference (TD) learning based on stochastic linear system models. TD-learning is a fundamental reinforcement learning (RL) to evaluate a given policy by estimating the corresponding value function for a Markov decision process. While there has been a series of successful works in theoretical analysis of TDlearning, it was not until recently that researchers found some guarantees on its statistical efficiency by developing finite-time error bounds. In this paper, we propose a simple control theoretic finite-time analysis of TD-learning, which exploits linear system models and standard notions in linear system communities. The proposed work provides new simple templets for RL analysis, and additional insights on TD-learning and RL based on ideas in control theory.

Regularized Q-learning

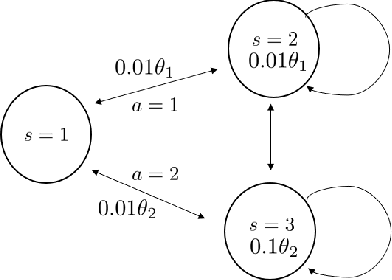
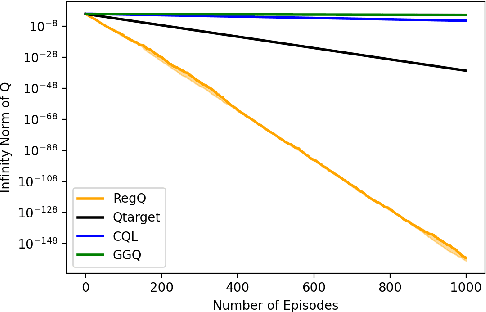
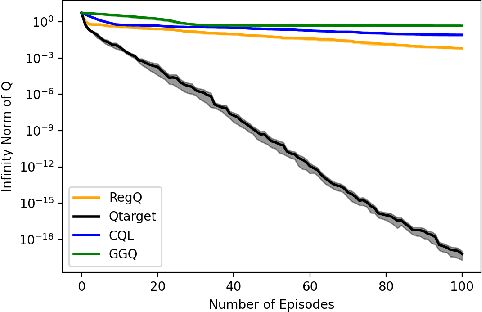
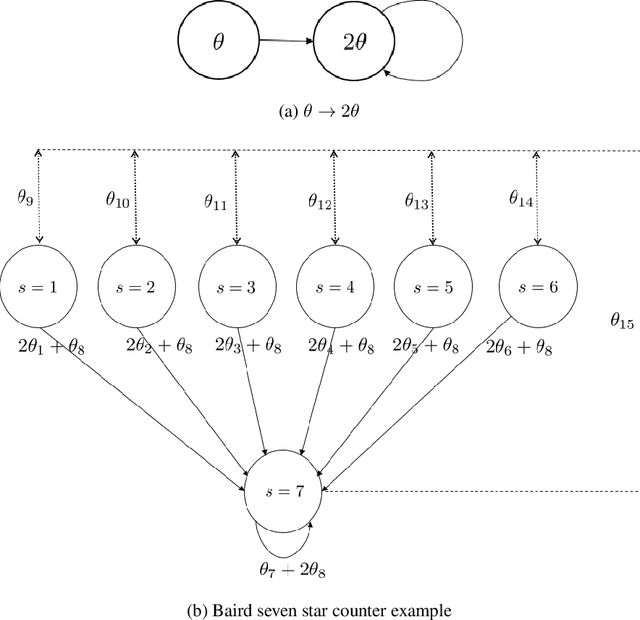
Q-learning is widely used algorithm in reinforcement learning community. Under the lookup table setting, its convergence is well established. However, its behavior is known to be unstable with the linear function approximation case. This paper develops a new Q-learning algorithm that converges when linear function approximation is used. We prove that simply adding an appropriate regularization term ensures convergence of the algorithm. We prove its stability using a recent analysis tool based on switching system models. Moreover, we experimentally show that it converges in environments where Q-learning with linear function approximation has known to diverge. We also provide an error bound on the solution where the algorithm converges.