Temporal Difference Learning with Experience Replay
Paper and Code
Jun 16, 2023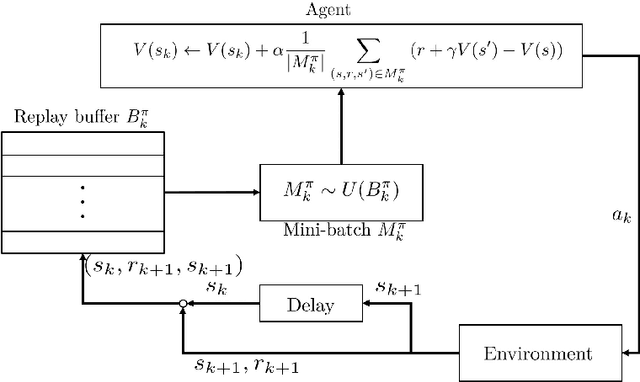


Temporal-difference (TD) learning is widely regarded as one of the most popular algorithms in reinforcement learning (RL). Despite its widespread use, it has only been recently that researchers have begun to actively study its finite time behavior, including the finite time bound on mean squared error and sample complexity. On the empirical side, experience replay has been a key ingredient in the success of deep RL algorithms, but its theoretical effects on RL have yet to be fully understood. In this paper, we present a simple decomposition of the Markovian noise terms and provide finite-time error bounds for TD-learning with experience replay. Specifically, under the Markovian observation model, we demonstrate that for both the averaged iterate and final iterate cases, the error term induced by a constant step-size can be effectively controlled by the size of the replay buffer and the mini-batch sampled from the experience replay buffer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge