Depen Morwani
Anytime Pretraining: Horizon-Free Learning-Rate Schedules with Weight Averaging
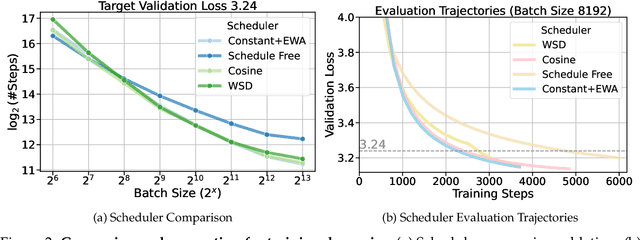
Feb 03, 2026Abstract:Large language models are increasingly trained in continual or open-ended settings, where the total training horizon is not known in advance. Despite this, most existing pretraining recipes are not anytime: they rely on horizon-dependent learning rate schedules and extensive tuning under a fixed compute budget. In this work, we provide a theoretical analysis demonstrating the existence of anytime learning schedules for overparameterized linear regression, and we highlight the central role of weight averaging - also known as model merging - in achieving the minimax convergence rates of stochastic gradient descent. We show that these anytime schedules polynomially decay with time, with the decay rate determined by the source and capacity conditions of the problem. Empirically, we evaluate 150M and 300M parameter language models trained at 1-32x Chinchilla scale, comparing constant learning rates with weight averaging and $1/\sqrt{t}$ schedules with weight averaging against a well-tuned cosine schedule. Across the full training range, the anytime schedules achieve comparable final loss to cosine decay. Taken together, our results suggest that weight averaging combined with simple, horizon-free step sizes offers a practical and effective anytime alternative to cosine learning rate schedules for large language model pretraining.
The Potential of Second-Order Optimization for LLMs: A Study with Full Gauss-Newton
Oct 10, 2025Abstract:Recent efforts to accelerate LLM pretraining have focused on computationally-efficient approximations that exploit second-order structure. This raises a key question for large-scale training: how much performance is forfeited by these approximations? To probe this question, we establish a practical upper bound on iteration complexity by applying full Gauss-Newton (GN) preconditioning to transformer models of up to 150M parameters. Our experiments show that full GN updates yield substantial gains over existing optimizers, achieving a 5.4x reduction in training iterations compared to strong baselines like SOAP and Muon. Furthermore, we find that a precise layerwise GN preconditioner, which ignores cross-layer information, nearly matches the performance of the full GN method. Collectively, our results suggest: (1) the GN approximation is highly effective for preconditioning, implying higher-order loss terms may not be critical for convergence speed; (2) the layerwise Hessian structure contains sufficient information to achieve most of these potential gains; and (3) a significant performance gap exists between current approximate methods and an idealized layerwise oracle.
A Simplified Analysis of SGD for Linear Regression with Weight Averaging
Jun 18, 2025Abstract:Theoretically understanding stochastic gradient descent (SGD) in overparameterized models has led to the development of several optimization algorithms that are widely used in practice today. Recent work by~\citet{zou2021benign} provides sharp rates for SGD optimization in linear regression using constant learning rate, both with and without tail iterate averaging, based on a bias-variance decomposition of the risk. In our work, we provide a simplified analysis recovering the same bias and variance bounds provided in~\citep{zou2021benign} based on simple linear algebra tools, bypassing the requirement to manipulate operators on positive semi-definite (PSD) matrices. We believe our work makes the analysis of SGD on linear regression very accessible and will be helpful in further analyzing mini-batching and learning rate scheduling, leading to improvements in the training of realistic models.
Connections between Schedule-Free Optimizers, AdEMAMix, and Accelerated SGD Variants
Feb 04, 2025


Abstract:Recent advancements in deep learning optimization have introduced new algorithms, such as Schedule-Free optimizers, AdEMAMix, MARS and Lion which modify traditional momentum mechanisms. In a separate line of work, theoretical acceleration of stochastic gradient descent (SGD) in noise-dominated regime has been achieved by decoupling the momentum coefficient from the current gradient's weight. In this paper, we establish explicit connections between these two lines of work. We substantiate our theoretical findings with preliminary experiments on a 150m language modeling task. We find that AdEMAMix, which most closely resembles accelerated versions of stochastic gradient descent, exhibits superior performance. Building on these insights, we introduce a modification to AdEMAMix, termed Simplified-AdEMAMix, which maintains the same performance as AdEMAMix across both large and small batch-size settings while eliminating the need for two different momentum terms. The code for Simplified-AdEMAMix is available on the repository: https://github.com/DepenM/Simplified-AdEMAMix/.
How Does Critical Batch Size Scale in Pre-training?
Oct 29, 2024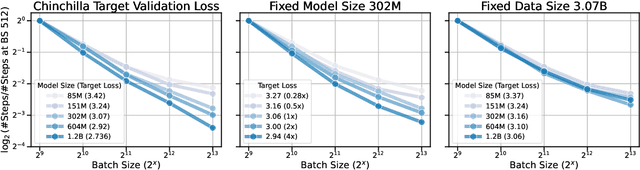

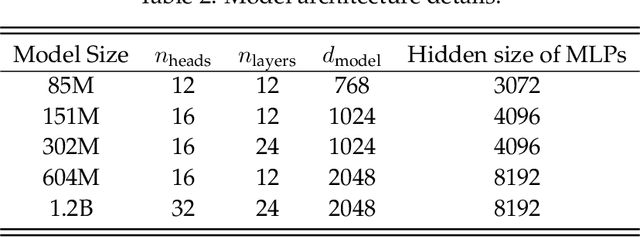
Abstract:Training large-scale models under given resources requires careful design of parallelism strategies. In particular, the efficiency notion of critical batch size, concerning the compromise between time and compute, marks the threshold beyond which greater data parallelism leads to diminishing returns. To operationalize it, we propose a measure of CBS and pre-train a series of auto-regressive language models, ranging from 85 million to 1.2 billion parameters, on the C4 dataset. Through extensive hyper-parameter sweeps and careful control on factors such as batch size, momentum, and learning rate along with its scheduling, we systematically investigate the impact of scale on CBS. Then we fit scaling laws with respect to model and data sizes to decouple their effects. Overall, our results demonstrate that CBS scales primarily with data size rather than model size, a finding we justify theoretically through the analysis of infinite-width limits of neural networks and infinite-dimensional least squares regression. Of independent interest, we highlight the importance of common hyper-parameter choices and strategies for studying large-scale pre-training beyond fixed training durations.
SOAP: Improving and Stabilizing Shampoo using Adam
Sep 17, 2024Abstract:There is growing evidence of the effectiveness of Shampoo, a higher-order preconditioning method, over Adam in deep learning optimization tasks. However, Shampoo's drawbacks include additional hyperparameters and computational overhead when compared to Adam, which only updates running averages of first- and second-moment quantities. This work establishes a formal connection between Shampoo (implemented with the 1/2 power) and Adafactor -- a memory-efficient approximation of Adam -- showing that Shampoo is equivalent to running Adafactor in the eigenbasis of Shampoo's preconditioner. This insight leads to the design of a simpler and computationally efficient algorithm: $\textbf{S}$hampo$\textbf{O}$ with $\textbf{A}$dam in the $\textbf{P}$reconditioner's eigenbasis (SOAP). With regards to improving Shampoo's computational efficiency, the most straightforward approach would be to simply compute Shampoo's eigendecomposition less frequently. Unfortunately, as our empirical results show, this leads to performance degradation that worsens with this frequency. SOAP mitigates this degradation by continually updating the running average of the second moment, just as Adam does, but in the current (slowly changing) coordinate basis. Furthermore, since SOAP is equivalent to running Adam in a rotated space, it introduces only one additional hyperparameter (the preconditioning frequency) compared to Adam. We empirically evaluate SOAP on language model pre-training with 360m and 660m sized models. In the large batch regime, SOAP reduces the number of iterations by over 40% and wall clock time by over 35% compared to AdamW, with approximately 20% improvements in both metrics compared to Shampoo. An implementation of SOAP is available at https://github.com/nikhilvyas/SOAP.
Deconstructing What Makes a Good Optimizer for Language Models
Jul 10, 2024Abstract:Training language models becomes increasingly expensive with scale, prompting numerous attempts to improve optimization efficiency. Despite these efforts, the Adam optimizer remains the most widely used, due to a prevailing view that it is the most effective approach. We aim to compare several optimization algorithms, including SGD, Adafactor, Adam, and Lion, in the context of autoregressive language modeling across a range of model sizes, hyperparameters, and architecture variants. Our findings indicate that, except for SGD, these algorithms all perform comparably both in their optimal performance and also in terms of how they fare across a wide range of hyperparameter choices. Our results suggest to practitioners that the choice of optimizer can be guided by practical considerations like memory constraints and ease of implementation, as no single algorithm emerged as a clear winner in terms of performance or stability to hyperparameter misspecification. Given our findings, we further dissect these approaches, examining two simplified versions of Adam: a) signed momentum (Signum) which we see recovers both the performance and hyperparameter stability of Adam and b) Adalayer, a layerwise variant of Adam which we introduce to study Adam's preconditioning. Examining Adalayer leads us to the conclusion that the largest impact of Adam's preconditioning is restricted to the last layer and LayerNorm parameters, and, perhaps surprisingly, the remaining layers can be trained with SGD.
A New Perspective on Shampoo's Preconditioner
Jun 25, 2024Abstract:Shampoo, a second-order optimization algorithm which uses a Kronecker product preconditioner, has recently garnered increasing attention from the machine learning community. The preconditioner used by Shampoo can be viewed either as an approximation of the Gauss--Newton component of the Hessian or the covariance matrix of the gradients maintained by Adagrad. We provide an explicit and novel connection between the $\textit{optimal}$ Kronecker product approximation of these matrices and the approximation made by Shampoo. Our connection highlights a subtle but common misconception about Shampoo's approximation. In particular, the $\textit{square}$ of the approximation used by the Shampoo optimizer is equivalent to a single step of the power iteration algorithm for computing the aforementioned optimal Kronecker product approximation. Across a variety of datasets and architectures we empirically demonstrate that this is close to the optimal Kronecker product approximation. Additionally, for the Hessian approximation viewpoint, we empirically study the impact of various practical tricks to make Shampoo more computationally efficient (such as using the batch gradient and the empirical Fisher) on the quality of Hessian approximation.
Feature emergence via margin maximization: case studies in algebraic tasks
Nov 13, 2023



Abstract:Understanding the internal representations learned by neural networks is a cornerstone challenge in the science of machine learning. While there have been significant recent strides in some cases towards understanding how neural networks implement specific target functions, this paper explores a complementary question -- why do networks arrive at particular computational strategies? Our inquiry focuses on the algebraic learning tasks of modular addition, sparse parities, and finite group operations. Our primary theoretical findings analytically characterize the features learned by stylized neural networks for these algebraic tasks. Notably, our main technique demonstrates how the principle of margin maximization alone can be used to fully specify the features learned by the network. Specifically, we prove that the trained networks utilize Fourier features to perform modular addition and employ features corresponding to irreducible group-theoretic representations to perform compositions in general groups, aligning closely with the empirical observations of Nanda et al. and Chughtai et al. More generally, we hope our techniques can help to foster a deeper understanding of why neural networks adopt specific computational strategies.
Beyond Implicit Bias: The Insignificance of SGD Noise in Online Learning
Jun 14, 2023Abstract:The success of SGD in deep learning has been ascribed by prior works to the implicit bias induced by high learning rate or small batch size ("SGD noise"). While prior works that focused on offline learning (i.e., multiple-epoch training), we study the impact of SGD noise on online (i.e., single epoch) learning. Through an extensive empirical analysis of image and language data, we demonstrate that large learning rate and small batch size do not confer any implicit bias advantages in online learning. In contrast to offline learning, the benefits of SGD noise in online learning are strictly computational, facilitating larger or more cost-effective gradient steps. Our work suggests that SGD in the online regime can be construed as taking noisy steps along the "golden path" of the noiseless gradient flow algorithm. We provide evidence to support this hypothesis by conducting experiments that reduce SGD noise during training and by measuring the pointwise functional distance between models trained with varying SGD noise levels, but at equivalent loss values. Our findings challenge the prevailing understanding of SGD and offer novel insights into its role in online learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge