Tractable Gaussian Phase Retrieval with Heavy Tails and Adversarial Corruption with Near-Linear Sample Complexity

Phase retrieval is the classical problem of recovering a signal $x^* \in \mathbb{R}^n$ from its noisy phaseless measurements $y_i = \langle a_i, x^* \rangle^2 + ζ_i$ (where $ζ_i$ denotes noise, and $a_i$ is the sensing vector) for $i \in [m]$. The problem of phase retrieval has a rich history, with a variety of applications such as optics, crystallography, heteroscedastic regression, astrophysics, etc. A major consideration in algorithms for phase retrieval is robustness against measurement errors. In recent breakthroughs in algorithmic robust statistics, efficient algorithms have been developed for several parameter estimation tasks such as mean estimation, covariance estimation, robust principal component analysis (PCA), etc. in the presence of heavy-tailed noise and adversarial corruptions. In this paper, we study efficient algorithms for robust phase retrieval with heavy-tailed noise when a constant fraction of both the measurements $y_i$ and the sensing vectors $a_i$ may be arbitrarily adversarially corrupted. For this problem, Buna and Rebeschini (AISTATS 2025) very recently gave an exponential time algorithm with sample complexity $O(n \log n)$. Their algorithm needs a robust spectral initialization, specifically, a robust estimate of the top eigenvector of a covariance matrix, which they deemed to be beyond known efficient algorithmic techniques (similar spectral initializations are a key ingredient of a large family of phase retrieval algorithms). In this work, we make a connection between robust spectral initialization and recent algorithmic advances in robust PCA, yielding the first polynomial-time algorithms for robust phase retrieval with both heavy-tailed noise and adversarial corruptions, in fact with near-linear (in $n$) sample complexity.

A unified law of robustness for Bregman divergence losses

In contemporary deep learning practice, models are often trained to near zero loss i.e. to nearly interpolate the training data. However, the number of parameters in the model is usually far more than the number of data points $n$, the theoretical minimum needed for interpolation: a phenomenon referred to as overparameterization. In an interesting piece of work that contributes to the considerable research that has been devoted to understand overparameterization, Bubeck, and Sellke showed that for a broad class of covariate distributions (specifically those satisfying a natural notion of concentration of measure), overparameterization is necessary for robust interpolation i.e. if the interpolating function is required to be Lipschitz. However, their robustness results were proved only in the setting of regression with square loss. In practice, however many other kinds of losses are used, e.g. cross entropy loss for classification. In this work, we generalize Bubeck and Selke's result to Bregman divergence losses, which form a common generalization of square loss and cross-entropy loss. Our generalization relies on identifying a bias variance-type decomposition that lies at the heart of the proof and Bubeck and Sellke.

Comparing skill of historical rainfall data based monsoon rainfall prediction in India with NCEP-NWP forecasts

In this draft we consider the problem of forecasting rainfall across India during the four monsoon months, one day as well as three days in advance. We train neural networks using historical daily gridded precipitation data for India obtained from IMD for the time period $1901- 2022$, at a spatial resolution of $1^{\circ} \times 1^{\circ}$. This is compared with the numerical weather prediction (NWP) forecasts obtained from NCEP (National Centre for Environmental Prediction) available for the period 2011-2022. We conduct a detailed country wide analysis and separately analyze some of the most populated cities in India. Our conclusion is that forecasts obtained by applying deep learning to historical rainfall data are more accurate compared to NWP forecasts as well as predictions based on persistence. On average, compared to our predictions, forecasts from NCEP-NWP model have about 34% higher error for a single day prediction, and over 68% higher error for a three day prediction. Similarly, persistence estimates report a 29% higher error in a single day forecast, and over 54% error in a three day forecast. We further observe that data up to 20 days in the past is useful in reducing errors of one and three day forecasts, when a transformer based learning architecture, and to a lesser extent when an LSTM is used. A key conclusion suggested by our preliminary analysis is that NWP forecasts can be substantially improved upon through more and diverse data relevant to monsoon prediction combined with carefully selected neural network architecture.

Simplicity Bias in 1-Hidden Layer Neural Networks

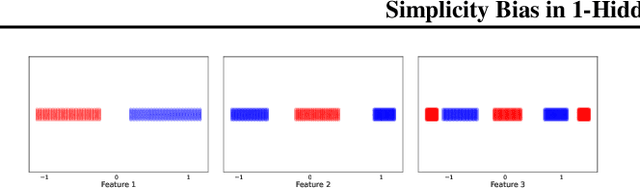
Recent works have demonstrated that neural networks exhibit extreme simplicity bias(SB). That is, they learn only the simplest features to solve a task at hand, even in the presence of other, more robust but more complex features. Due to the lack of a general and rigorous definition of features, these works showcase SB on semi-synthetic datasets such as Color-MNIST, MNIST-CIFAR where defining features is relatively easier. In this work, we rigorously define as well as thoroughly establish SB for one hidden layer neural networks. More concretely, (i) we define SB as the network essentially being a function of a low dimensional projection of the inputs (ii) theoretically, we show that when the data is linearly separable, the network primarily depends on only the linearly separable ($1$-dimensional) subspace even in the presence of an arbitrarily large number of other, more complex features which could have led to a significantly more robust classifier, (iii) empirically, we show that models trained on real datasets such as Imagenette and Waterbirds-Landbirds indeed depend on a low dimensional projection of the inputs, thereby demonstrating SB on these datasets, iv) finally, we present a natural ensemble approach that encourages diversity in models by training successive models on features not used by earlier models, and demonstrate that it yields models that are significantly more robust to Gaussian noise.