Innovation: An Almost Characterization of Hallucination

Hallucination is a central limitation of large language models (LLMs), and substantial effort has been devoted to understanding and mitigating it. Towards this, Kalai and Vempala (STOC 2024) introduced a probabilistic framework formalizing calibration and hallucination, and showed that, with high probability, calibrated LLMs hallucinate roughly at the rate of the "missing mass", a measure of how incomplete the training data is relative to its source. This raises two fundamental questions: (i) what property of a calibrated LLM makes hallucinations unavoidable? and (ii) can hallucinations be avoided by giving up calibration? We answer these questions by introducing a simpler property we call innovation that measures the tendency of a model to produce outputs outside the training data. We show that innovation is implied by the condition for hallucination identified by Kalai and Vempala, and, further, that it is an almost characterization of hallucination: hallucination implies innovation, and conversely, innovation implies hallucination with high probability. We also provide lower bounds on the hallucination rate based on the "innovation rate", and by relating innovation rate back to missing mass, we obtain new hallucination rate lower bounds based on missing mass that extend the results of Kalai and Vempala.

A unified law of robustness for Bregman divergence losses

In contemporary deep learning practice, models are often trained to near zero loss i.e. to nearly interpolate the training data. However, the number of parameters in the model is usually far more than the number of data points $n$, the theoretical minimum needed for interpolation: a phenomenon referred to as overparameterization. In an interesting piece of work that contributes to the considerable research that has been devoted to understand overparameterization, Bubeck, and Sellke showed that for a broad class of covariate distributions (specifically those satisfying a natural notion of concentration of measure), overparameterization is necessary for robust interpolation i.e. if the interpolating function is required to be Lipschitz. However, their robustness results were proved only in the setting of regression with square loss. In practice, however many other kinds of losses are used, e.g. cross entropy loss for classification. In this work, we generalize Bubeck and Selke's result to Bregman divergence losses, which form a common generalization of square loss and cross-entropy loss. Our generalization relies on identifying a bias variance-type decomposition that lies at the heart of the proof and Bubeck and Sellke.

Almost Optimal Universal Lower Bound for Learning Causal DAGs with Atomic Interventions

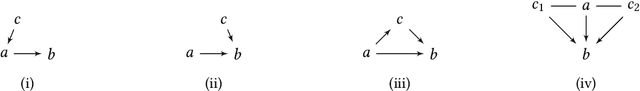
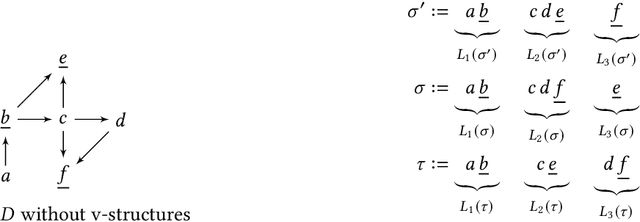
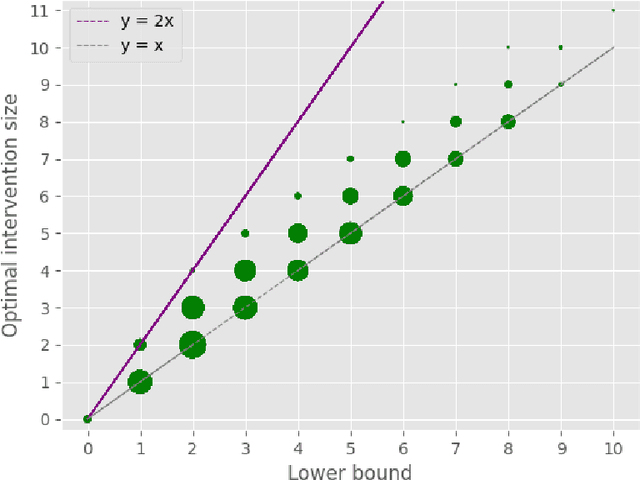
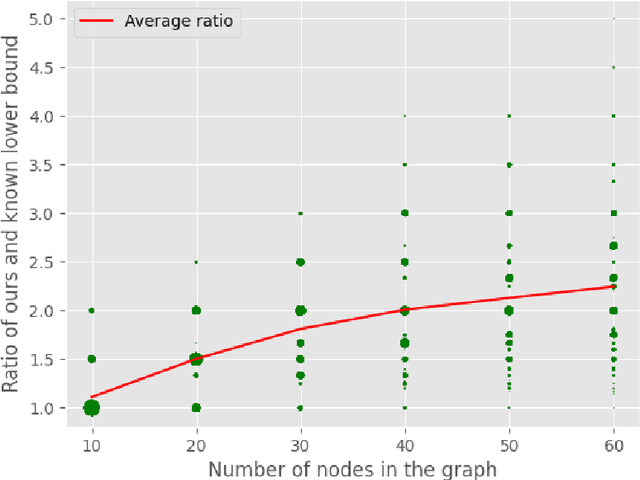
A well-studied challenge that arises in the structure learning problem of causal directed acyclic graphs (DAG) is that using observational data, one can only learn the graph up to a "Markov equivalence class" (MEC). The remaining undirected edges have to be oriented using interventions, which can be very expensive to perform in applications. Thus, the problem of minimizing the number of interventions needed to fully orient the MEC has received a lot of recent attention, and is also the focus of this work. We prove two main results. The first is a new universal lower bound on the number of atomic interventions that any algorithm (whether active or passive) would need to perform in order to orient a given MEC. Our second result shows that this bound is, in fact, within a factor of two of the size of the smallest set of atomic interventions that can orient the MEC. Our lower bound is provably better than previously known lower bounds. The proof of our lower bound is based on the new notion of clique-block shared-parents (CBSP) orderings, which are topological orderings of DAGs without v-structures and satisfy certain special properties. Further, using simulations on synthetic graphs and by giving examples of special graph families, we show that our bound is often significantly better.