CoINS: Counterfactual Interactive Navigation via Skill-Aware VLM

Recent Vision-Language Models (VLMs) have demonstrated significant potential in robotic planning. However, they typically function as semantic reasoners, lacking an intrinsic understanding of the specific robot's physical capabilities. This limitation is particularly critical in interactive navigation, where robots must actively modify cluttered environments to create traversable paths. Existing VLM-based navigators are predominantly confined to passive obstacle avoidance, failing to reason about when and how to interact with objects to clear blocked paths. To bridge this gap, we propose Counterfactual Interactive Navigation via Skill-aware VLM (CoINS), a hierarchical framework that integrates skill-aware reasoning and robust low-level execution. Specifically, we fine-tune a VLM, named InterNav-VLM, which incorporates skill affordance and concrete constraint parameters into the input context and grounds them into a metric-scale environmental representation. By internalizing the logic of counterfactual reasoning through fine-tuning on the proposed InterNav dataset, the model learns to implicitly evaluate the causal effects of object removal on navigation connectivity, thereby determining interaction necessity and target selection. To execute the generated high-level plans, we develop a comprehensive skill library through reinforcement learning, specifically introducing traversability-oriented strategies to manipulate diverse objects for path clearance. A systematic benchmark in Isaac Sim is proposed to evaluate both the reasoning and execution aspects of interactive navigation. Extensive simulations and real-world experiments demonstrate that CoINS significantly outperforms representative baselines, achieving a 17\% higher overall success rate and over 80\% improvement in complex long-horizon scenarios compared to the best-performing baseline

Basic Inequalities for First-Order Optimization with Applications to Statistical Risk Analysis

We introduce \textit{basic inequalities} for first-order iterative optimization algorithms, forming a simple and versatile framework that connects implicit and explicit regularization. While related inequalities appear in the literature, we isolate and highlight a specific form and develop it as a well-rounded tool for statistical analysis. Let $f$ denote the objective function to be optimized. Given a first-order iterative algorithm initialized at $θ_0$ with current iterate $θ_T$, the basic inequality upper bounds $f(θ_T)-f(z)$ for any reference point $z$ in terms of the accumulated step sizes and the distances between $θ_0$, $θ_T$, and $z$. The bound translates the number of iterations into an effective regularization coefficient in the loss function. We demonstrate this framework through analyses of training dynamics and prediction risk bounds. In addition to revisiting and refining known results on gradient descent, we provide new results for mirror descent with Bregman divergence projection, for generalized linear models trained by gradient descent and exponentiated gradient descent, and for randomized predictors. We illustrate and supplement these theoretical findings with experiments on generalized linear models.

ReSPIRe: Informative and Reusable Belief Tree Search for Robot Probabilistic Search and Tracking in Unknown Environments

Target search and tracking (SAT) is a fundamental problem for various robotic applications such as search and rescue and environmental exploration. This paper proposes an informative trajectory planning approach, namely ReSPIRe, for SAT in unknown cluttered environments under considerably inaccurate prior target information and limited sensing field of view. We first develop a novel sigma point-based approximation approach to fast and accurately estimate mutual information reward under non-Gaussian belief distributions, utilizing informative sampling in state and observation spaces to mitigate the computational intractability of integral calculation. To tackle significant uncertainty associated with inadequate prior target information, we propose the hierarchical particle structure in ReSPIRe, which not only extracts critical particles for global route guidance, but also adjusts the particle number adaptively for planning efficiency. Building upon the hierarchical structure, we develop the reusable belief tree search approach to build a policy tree for online trajectory planning under uncertainty, which reuses rollout evaluation to improve planning efficiency. Extensive simulations and real-world experiments demonstrate that ReSPIRe outperforms representative benchmark methods with smaller MI approximation error, higher search efficiency, and more stable tracking performance, while maintaining outstanding computational efficiency.

SwarmDiff: Swarm Robotic Trajectory Planning in Cluttered Environments via Diffusion Transformer

Swarm robotic trajectory planning faces challenges in computational efficiency, scalability, and safety, particularly in complex, obstacle-dense environments. To address these issues, we propose SwarmDiff, a hierarchical and scalable generative framework for swarm robots. We model the swarm's macroscopic state using Probability Density Functions (PDFs) and leverage conditional diffusion models to generate risk-aware macroscopic trajectory distributions, which then guide the generation of individual robot trajectories at the microscopic level. To ensure a balance between the swarm's optimal transportation and risk awareness, we integrate Wasserstein metrics and Conditional Value at Risk (CVaR). Additionally, we introduce a Diffusion Transformer (DiT) to improve sampling efficiency and generation quality by capturing long-range dependencies. Extensive simulations and real-world experiments demonstrate that SwarmDiff outperforms existing methods in computational efficiency, trajectory validity, and scalability, making it a reliable solution for swarm robotic trajectory planning.

Adaptive Interactive Navigation of Quadruped Robots using Large Language Models

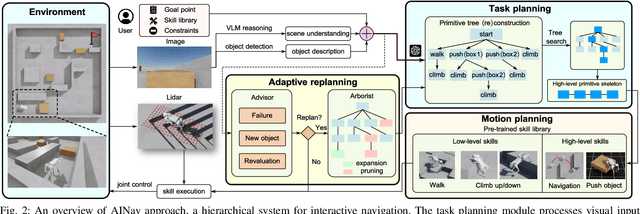
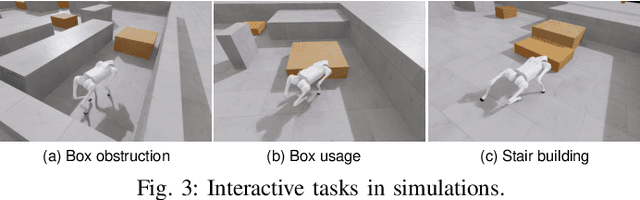
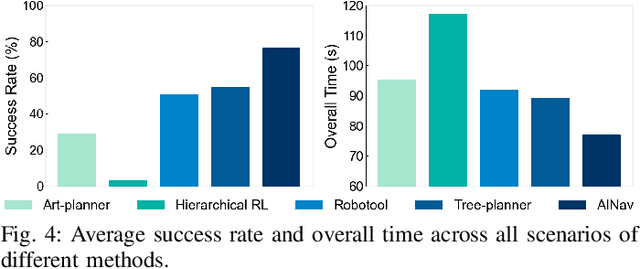
Robotic navigation in complex environments remains a critical research challenge. Traditional navigation methods focus on optimal trajectory generation within free space, struggling in environments lacking viable paths to the goal, such as disaster zones or cluttered warehouses. To address this gap, we propose an adaptive interactive navigation approach that proactively interacts with environments to create feasible paths to reach originally unavailable goals. Specifically, we present a primitive tree for task planning with large language models (LLMs), facilitating effective reasoning to determine interaction objects and sequences. To ensure robust subtask execution, we adopt reinforcement learning to pre-train a comprehensive skill library containing versatile locomotion and interaction behaviors for motion planning. Furthermore, we introduce an adaptive replanning method featuring two LLM-based modules: an advisor serving as a flexible replanning trigger and an arborist for autonomous plan adjustment. Integrated with the tree structure, the replanning mechanism allows for convenient node addition and pruning, enabling rapid plan modification in unknown environments. Comprehensive simulations and experiments have demonstrated our method's effectiveness and adaptivity in diverse scenarios. The supplementary video is available at page: https://youtu.be/W5ttPnSap2g.

Implicit Bias of Gradient Descent for Non-Homogeneous Deep Networks

We establish the asymptotic implicit bias of gradient descent (GD) for generic non-homogeneous deep networks under exponential loss. Specifically, we characterize three key properties of GD iterates starting from a sufficiently small empirical risk, where the threshold is determined by a measure of the network's non-homogeneity. First, we show that a normalized margin induced by the GD iterates increases nearly monotonically. Second, we prove that while the norm of the GD iterates diverges to infinity, the iterates themselves converge in direction. Finally, we establish that this directional limit satisfies the Karush-Kuhn-Tucker (KKT) conditions of a margin maximization problem. Prior works on implicit bias have focused exclusively on homogeneous networks; in contrast, our results apply to a broad class of non-homogeneous networks satisfying a mild near-homogeneity condition. In particular, our results apply to networks with residual connections and non-homogeneous activation functions, thereby resolving an open problem posed by Ji and Telgarsky (2020).

CAMON: Cooperative Agents for Multi-Object Navigation with LLM-based Conversations

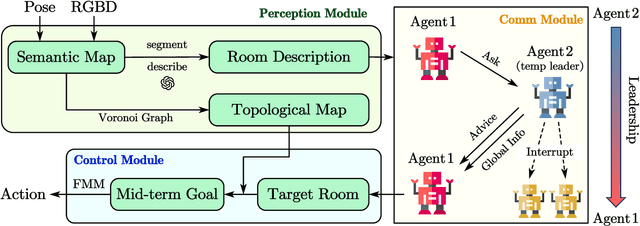
Visual navigation tasks are critical for household service robots. As these tasks become increasingly complex, effective communication and collaboration among multiple robots become imperative to ensure successful completion. In recent years, large language models (LLMs) have exhibited remarkable comprehension and planning abilities in the context of embodied agents. However, their application in household scenarios, specifically in the use of multiple agents collaborating to complete complex navigation tasks through communication, remains unexplored. Therefore, this paper proposes a framework for decentralized multi-agent navigation, leveraging LLM-enabled communication and collaboration. By designing the communication-triggered dynamic leadership organization structure, we achieve faster team consensus with fewer communication instances, leading to better navigation effectiveness and collaborative exploration efficiency. With the proposed novel communication scheme, our framework promises to be conflict-free and robust in multi-object navigation tasks, even when there is a surge in team size.

Which exceptional low-dimensional projections of a Gaussian point cloud can be found in polynomial time?

Given $d$-dimensional standard Gaussian vectors $\boldsymbol{x}_1,\dots, \boldsymbol{x}_n$, we consider the set of all empirical distributions of its $m$-dimensional projections, for $m$ a fixed constant. Diaconis and Freedman (1984) proved that, if $n/d\to \infty$, all such distributions converge to the standard Gaussian distribution. In contrast, we study the proportional asymptotics, whereby $n,d\to \infty$ with $n/d\to \alpha \in (0, \infty)$. In this case, the projection of the data points along a typical random subspace is again Gaussian, but the set $\mathscr{F}_{m,\alpha}$ of all probability distributions that are asymptotically feasible as $m$-dimensional projections contains non-Gaussian distributions corresponding to exceptional subspaces. Non-rigorous methods from statistical physics yield an indirect characterization of $\mathscr{F}_{m,\alpha}$ in terms of a generalized Parisi formula. Motivated by the goal of putting this formula on a rigorous basis, and to understand whether these projections can be found efficiently, we study the subset $\mathscr{F}^{\rm alg}_{m,\alpha}\subseteq \mathscr{F}_{m,\alpha}$ of distributions that can be realized by a class of iterative algorithms. We prove that this set is characterized by a certain stochastic optimal control problem, and obtain a dual characterization of this problem in terms of a variational principle that extends Parisi's formula. As a byproduct, we obtain computationally achievable values for a class of random optimization problems including `generalized spherical perceptron' models.

ASPIRe: An Informative Trajectory Planner with Mutual Information Approximation for Target Search and Tracking

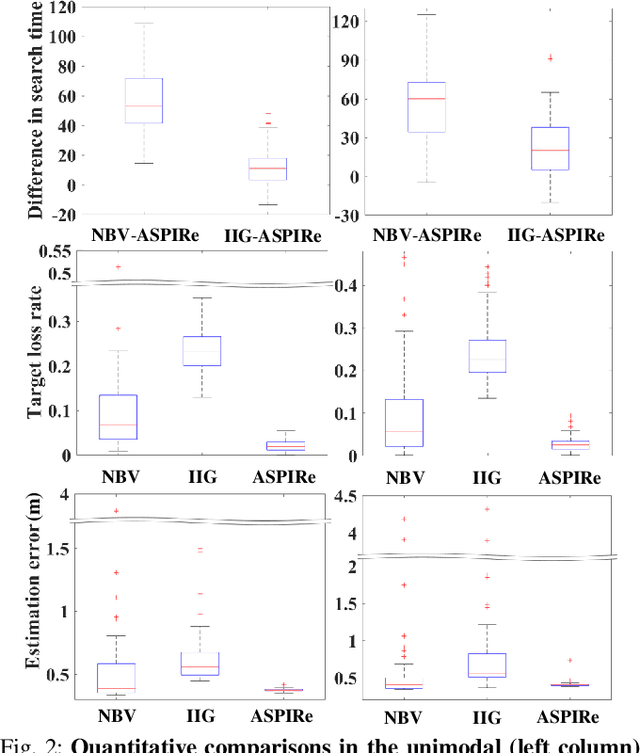
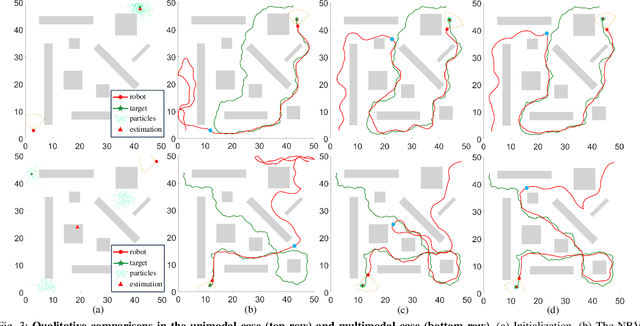
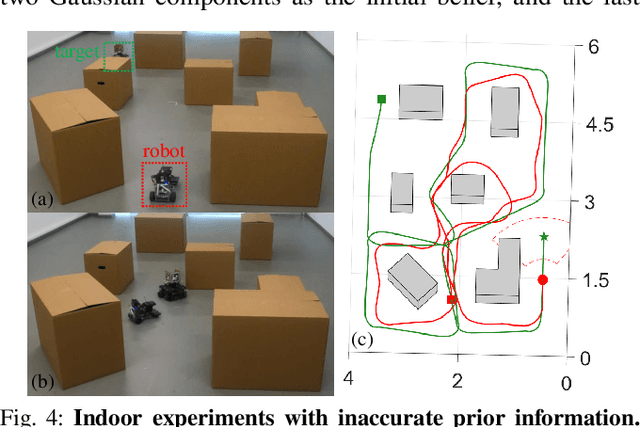
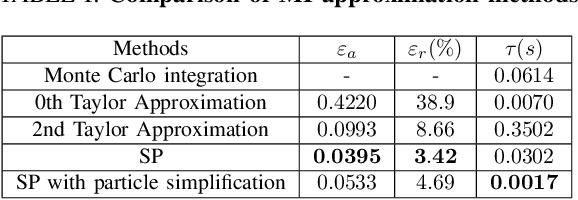
This paper proposes an informative trajectory planning approach, namely, \textit{adaptive particle filter tree with sigma point-based mutual information reward approximation} (ASPIRe), for mobile target search and tracking (SAT) in cluttered environments with limited sensing field of view. We develop a novel sigma point-based approximation to accurately estimate mutual information (MI) for general, non-Gaussian distributions utilizing particle representation of the belief state, while simultaneously maintaining high computational efficiency. Building upon the MI approximation, we develop the Adaptive Particle Filter Tree (APFT) approach with MI as the reward, which features belief state tree nodes for informative trajectory planning in continuous state and measurement spaces. An adaptive criterion is proposed in APFT to adjust the planning horizon based on the expected information gain. Simulations and physical experiments demonstrate that ASPIRe achieves real-time computation and outperforms benchmark methods in terms of both search efficiency and estimation accuracy.

SwarmPRM: Probabilistic Roadmap Motion Planning for Swarm Robotic Systems

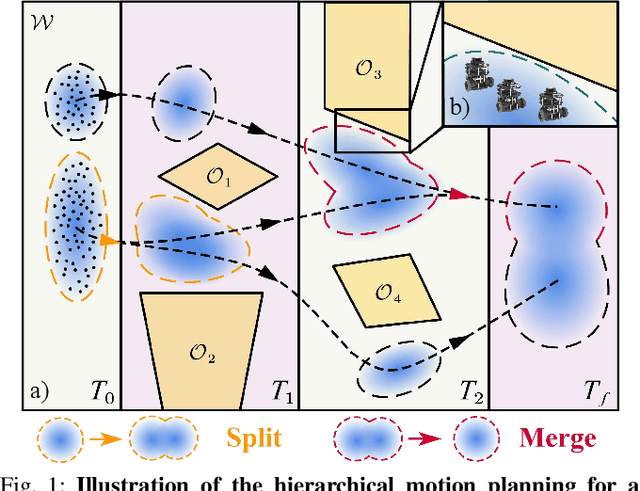
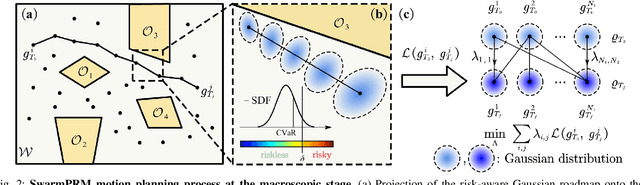
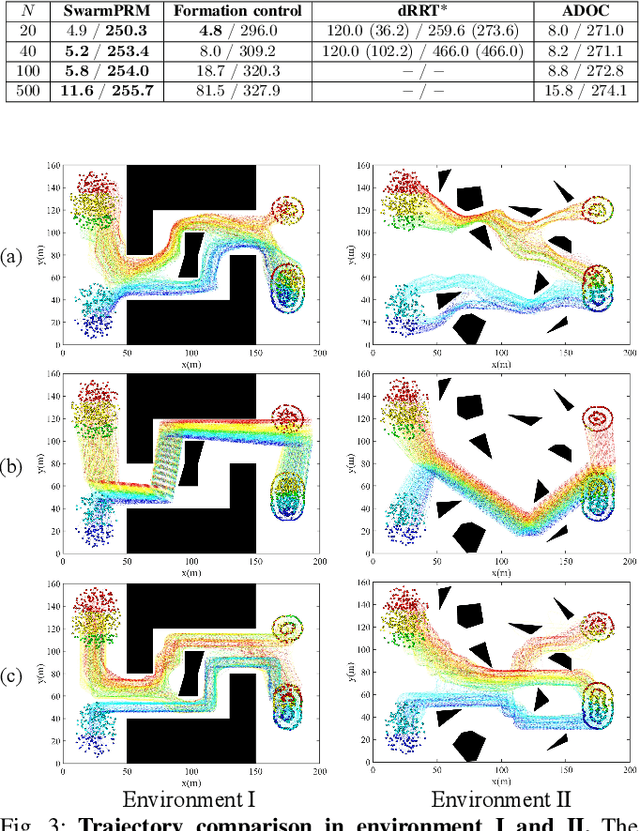
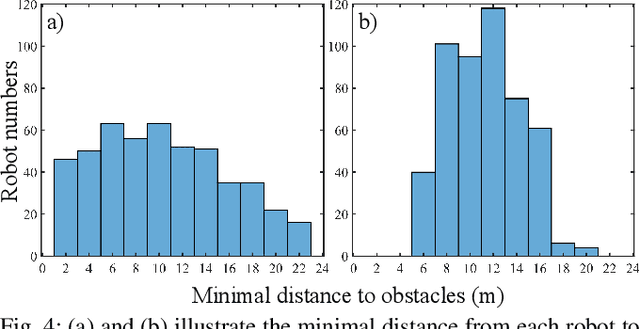
Swarm robotic systems consisting of large-scale cooperative agents hold promise for performing autonomous tasks in diverse fields. However, existing planning strategies for swarm robotic systems often encounter a trade-off between scalability and solution quality. We introduce here SwarmPRM, a hierarchical, highly scalable, computationally efficient, and risk-aware sampling-based motion planning approach for swarm robotic systems, which is asymptotically optimal under mild assumptions. We employ probability density functions (PDFs) to represent the swarm's macroscopic state and utilize optimal mass transport (OMT) theory to measure the swarm's cost to go. A risk-aware Gaussian roadmap is constructed wherein each node encapsulates a distinct PDF and conditional-value-at-risk (CVaR) is employed to assess the collision risk, facilitating the generation of macroscopic PDFs in Wasserstein-GMM space. Extensive simulations demonstrate that the proposed approach outperforms state-of-the-art methods in terms of computational efficiency and the average travelling distance.