DADP: Domain Adaptive Diffusion Policy

Learning domain adaptive policies that can generalize to unseen transition dynamics, remains a fundamental challenge in learning-based control. Substantial progress has been made through domain representation learning to capture domain-specific information, thus enabling domain-aware decision making. We analyze the process of learning domain representations through dynamical prediction and find that selecting contexts adjacent to the current step causes the learned representations to entangle static domain information with varying dynamical properties. Such mixture can confuse the conditioned policy, thereby constraining zero-shot adaptation. To tackle the challenge, we propose DADP (Domain Adaptive Diffusion Policy), which achieves robust adaptation through unsupervised disentanglement and domain-aware diffusion injection. First, we introduce Lagged Context Dynamical Prediction, a strategy that conditions future state estimation on a historical offset context; by increasing this temporal gap, we unsupervisedly disentangle static domain representations by filtering out transient properties. Second, we integrate the learned domain representations directly into the generative process by biasing the prior distribution and reformulating the diffusion target. Extensive experiments on challenging benchmarks across locomotion and manipulation demonstrate the superior performance, and the generalizability of DADP over prior methods. More visualization results are available on the https://outsider86.github.io/DomainAdaptiveDiffusionPolicy/.

SwarmPRM: Probabilistic Roadmap Motion Planning for Swarm Robotic Systems

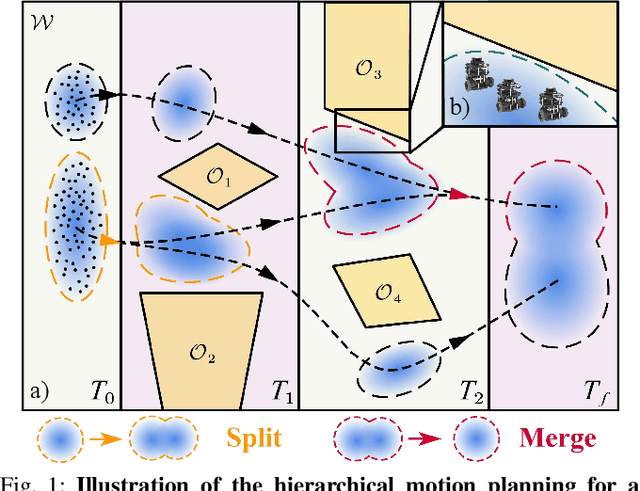
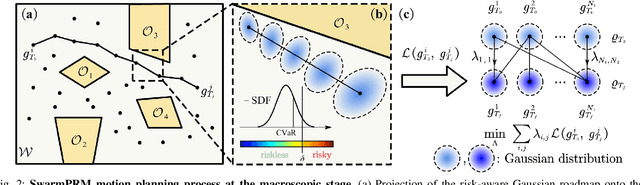
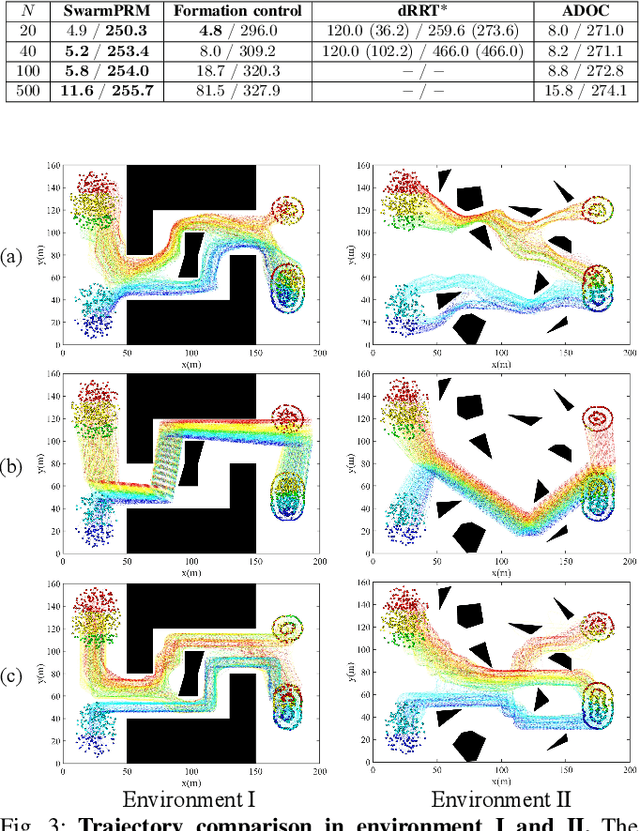
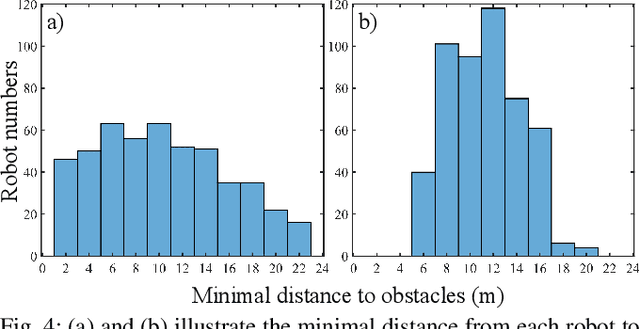
Swarm robotic systems consisting of large-scale cooperative agents hold promise for performing autonomous tasks in diverse fields. However, existing planning strategies for swarm robotic systems often encounter a trade-off between scalability and solution quality. We introduce here SwarmPRM, a hierarchical, highly scalable, computationally efficient, and risk-aware sampling-based motion planning approach for swarm robotic systems, which is asymptotically optimal under mild assumptions. We employ probability density functions (PDFs) to represent the swarm's macroscopic state and utilize optimal mass transport (OMT) theory to measure the swarm's cost to go. A risk-aware Gaussian roadmap is constructed wherein each node encapsulates a distinct PDF and conditional-value-at-risk (CVaR) is employed to assess the collision risk, facilitating the generation of macroscopic PDFs in Wasserstein-GMM space. Extensive simulations demonstrate that the proposed approach outperforms state-of-the-art methods in terms of computational efficiency and the average travelling distance.