NTIRE 2024 Challenge on Low Light Image Enhancement: Methods and Results

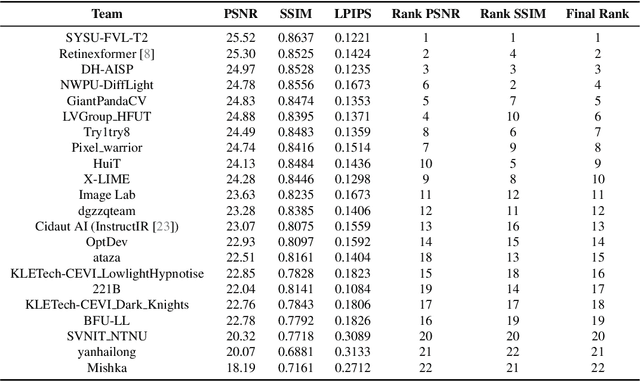
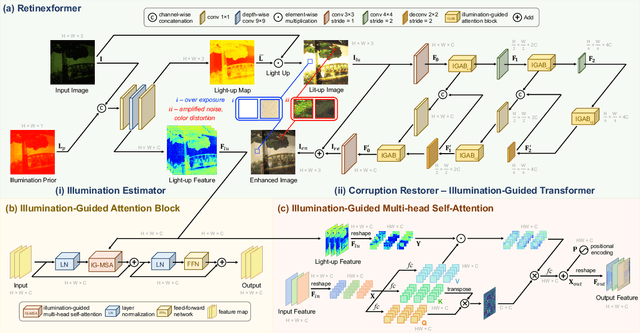
This paper reviews the NTIRE 2024 low light image enhancement challenge, highlighting the proposed solutions and results. The aim of this challenge is to discover an effective network design or solution capable of generating brighter, clearer, and visually appealing results when dealing with a variety of conditions, including ultra-high resolution (4K and beyond), non-uniform illumination, backlighting, extreme darkness, and night scenes. A notable total of 428 participants registered for the challenge, with 22 teams ultimately making valid submissions. This paper meticulously evaluates the state-of-the-art advancements in enhancing low-light images, reflecting the significant progress and creativity in this field.

PreGSU-A Generalized Traffic Scene Understanding Model for Autonomous Driving based on Pre-trained Graph Attention Network

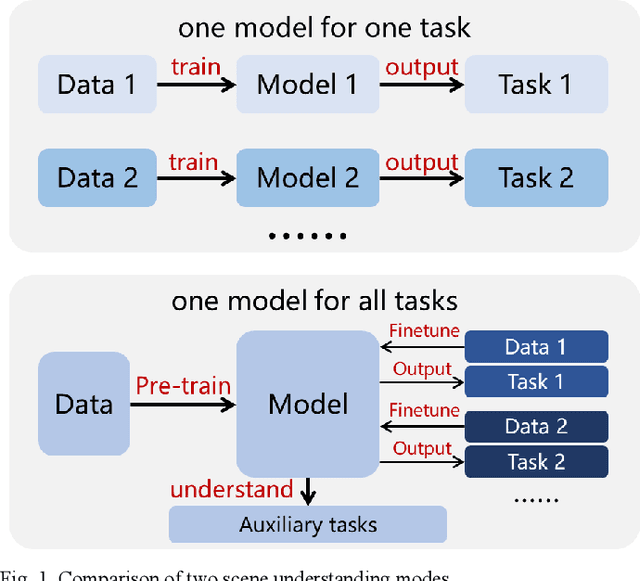
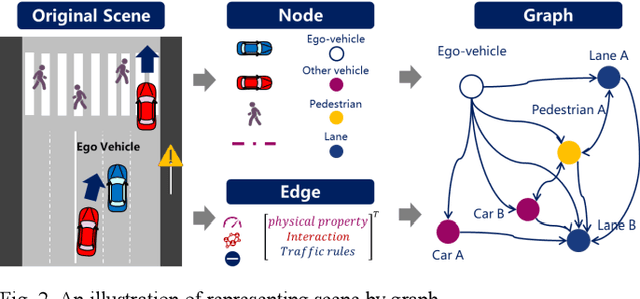
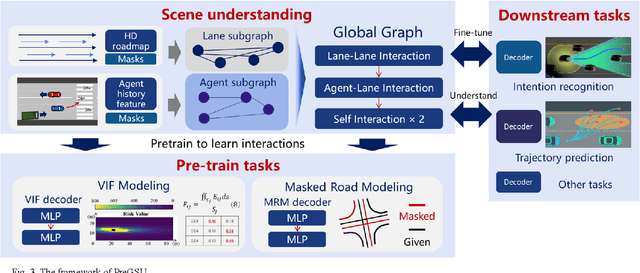
Scene understanding, defined as learning, extraction, and representation of interactions among traffic elements, is one of the critical challenges toward high-level autonomous driving (AD). Current scene understanding methods mainly focus on one concrete single task, such as trajectory prediction and risk level evaluation. Although they perform well on specific metrics, the generalization ability is insufficient to adapt to the real traffic complexity and downstream demand diversity. In this study, we propose PreGSU, a generalized pre-trained scene understanding model based on graph attention network to learn the universal interaction and reasoning of traffic scenes to support various downstream tasks. After the feature engineering and sub-graph module, all elements are embedded as nodes to form a dynamic weighted graph. Then, four graph attention layers are applied to learn the relationships among agents and lanes. In the pre-train phase, the understanding model is trained on two self-supervised tasks: Virtual Interaction Force (VIF) modeling and Masked Road Modeling (MRM). Based on the artificial potential field theory, VIF modeling enables PreGSU to capture the agent-to-agent interactions while MRM extracts agent-to-road connections. In the fine-tuning process, the pre-trained parameters are loaded to derive detailed understanding outputs. We conduct validation experiments on two downstream tasks, i.e., trajectory prediction in urban scenario, and intention recognition in highway scenario, to verify the generalized ability and understanding ability. Results show that compared with the baselines, PreGSU achieves better accuracy on both tasks, indicating the potential to be generalized to various scenes and targets. Ablation study shows the effectiveness of pre-train task design.

Joint Pedestrian Trajectory Prediction through Posterior Sampling

Joint pedestrian trajectory prediction has long grappled with the inherent unpredictability of human behaviors. Recent investigations employing variants of conditional diffusion models in trajectory prediction have exhibited notable success. Nevertheless, the heavy dependence on accurate historical data results in their vulnerability to noise disturbances and data incompleteness. To improve the robustness and reliability, we introduce the Guided Full Trajectory Diffuser (GFTD), a novel diffusion model framework that captures the joint full (historical and future) trajectory distribution. By learning from the full trajectory, GFTD can recover the noisy and missing data, hence improving the robustness. In addition, GFTD can adapt to data imperfections without additional training requirements, leveraging posterior sampling for reliable prediction and controllable generation. Our approach not only simplifies the prediction process but also enhances generalizability in scenarios with noise and incomplete inputs. Through rigorous experimental evaluation, GFTD exhibits superior performance in both trajectory prediction and controllable generation.

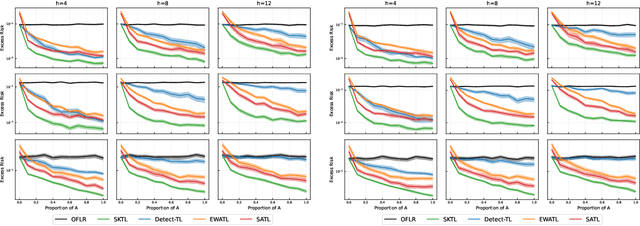
Smoothness Adaptive Hypothesis Transfer Learning

Many existing two-phase kernel-based hypothesis transfer learning algorithms employ the same kernel regularization across phases and rely on the known smoothness of functions to obtain optimality. Therefore, they fail to adapt to the varying and unknown smoothness between the target/source and their offset in practice. In this paper, we address these problems by proposing Smoothness Adaptive Transfer Learning (SATL), a two-phase kernel ridge regression(KRR)-based algorithm. We first prove that employing the misspecified fixed bandwidth Gaussian kernel in target-only KRR learning can achieve minimax optimality and derive an adaptive procedure to the unknown Sobolev smoothness. Leveraging these results, SATL employs Gaussian kernels in both phases so that the estimators can adapt to the unknown smoothness of the target/source and their offset function. We derive the minimax lower bound of the learning problem in excess risk and show that SATL enjoys a matching upper bound up to a logarithmic factor. The minimax convergence rate sheds light on the factors influencing transfer dynamics and demonstrates the superiority of SATL compared to non-transfer learning settings. While our main objective is a theoretical analysis, we also conduct several experiments to confirm our results.

Differentially Private Functional Summaries via the Independent Component Laplace Process

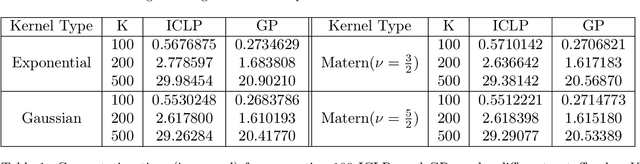
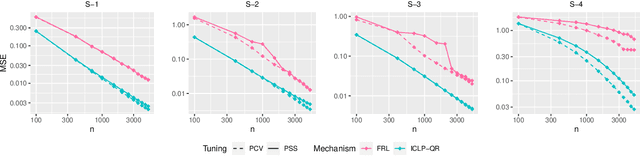
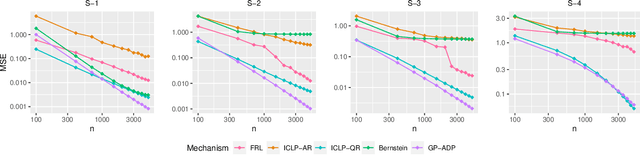
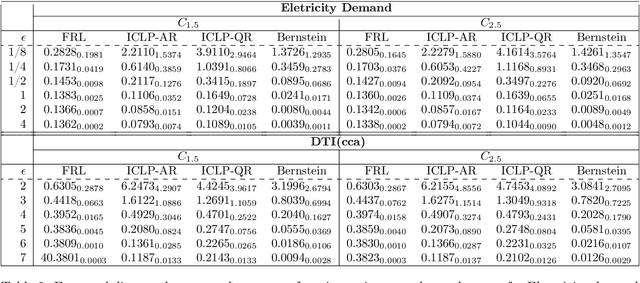
In this work, we propose a new mechanism for releasing differentially private functional summaries called the Independent Component Laplace Process, or ICLP, mechanism. By treating the functional summaries of interest as truly infinite-dimensional objects and perturbing them with the ICLP noise, this new mechanism relaxes assumptions on data trajectories and preserves higher utility compared to classical finite-dimensional subspace embedding approaches in the literature. We establish the feasibility of the proposed mechanism in multiple function spaces. Several statistical estimation problems are considered, and we demonstrate by slightly over-smoothing the summary, the privacy cost will not dominate the statistical error and is asymptotically negligible. Numerical experiments on synthetic and real datasets demonstrate the efficacy of the proposed mechanism.

On Transfer Learning in Functional Linear Regression

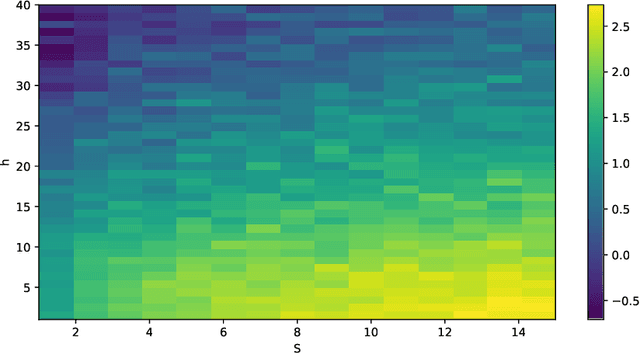
This work studies the problem of transfer learning under the functional linear model framework, which aims to improve the fit of the target model by leveraging the knowledge from related source models. We measure the relatedness between target and source models using Reproducing Kernel Hilbert Spaces, allowing the type of knowledge being transferred to be interpreted by the structure of the spaces. Two algorithms are proposed: one transfers knowledge when the index of transferable sources is known, while the other one utilizes aggregation to achieve knowledge transfer without prior information about the sources. Furthermore, we establish the optimal convergence rates for excess risk, making the statistical gain via transfer learning mathematically provable. The effectiveness of the proposed algorithms is demonstrated on synthetic data as well as real financial data.