On Transfer Learning in Functional Linear Regression
Paper and Code
Jun 09, 2022
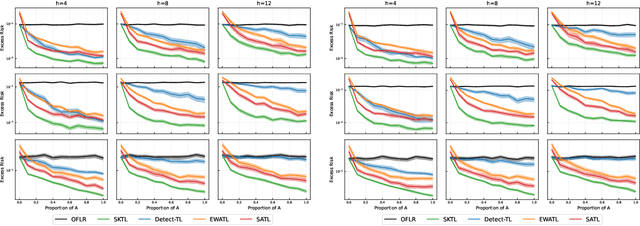
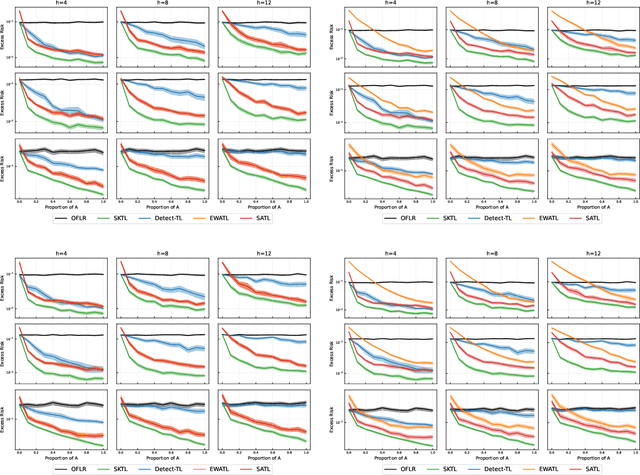
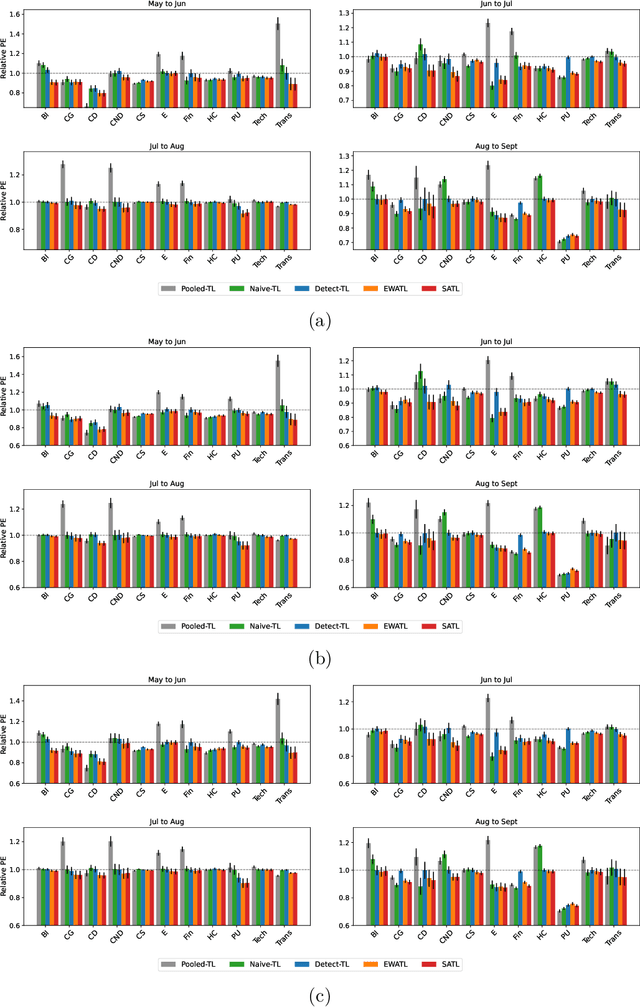
This work studies the problem of transfer learning under the functional linear model framework, which aims to improve the fit of the target model by leveraging the knowledge from related source models. We measure the relatedness between target and source models using Reproducing Kernel Hilbert Spaces, allowing the type of knowledge being transferred to be interpreted by the structure of the spaces. Two algorithms are proposed: one transfers knowledge when the index of transferable sources is known, while the other one utilizes aggregation to achieve knowledge transfer without prior information about the sources. Furthermore, we establish the optimal convergence rates for excess risk, making the statistical gain via transfer learning mathematically provable. The effectiveness of the proposed algorithms is demonstrated on synthetic data as well as real financial data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge