Harnessing Vision-Language Models for Time Series Anomaly Detection

Time-series anomaly detection (TSAD) has played a vital role in a variety of fields, including healthcare, finance, and industrial monitoring. Prior methods, which mainly focus on training domain-specific models on numerical data, lack the visual-temporal reasoning capacity that human experts have to identify contextual anomalies. To fill this gap, we explore a solution based on vision language models (VLMs). Recent studies have shown the ability of VLMs for visual reasoning tasks, yet their direct application to time series has fallen short on both accuracy and efficiency. To harness the power of VLMs for TSAD, we propose a two-stage solution, with (1) ViT4TS, a vision-screening stage built on a relatively lightweight pretrained vision encoder, which leverages 2-D time-series representations to accurately localize candidate anomalies; (2) VLM4TS, a VLM-based stage that integrates global temporal context and VLM reasoning capacity to refine the detection upon the candidates provided by ViT4TS. We show that without any time-series training, VLM4TS outperforms time-series pretrained and from-scratch baselines in most cases, yielding a 24.6 percent improvement in F1-max score over the best baseline. Moreover, VLM4TS also consistently outperforms existing language-model-based TSAD methods and is on average 36 times more efficient in token usage.

M$^2$AD: Multi-Sensor Multi-System Anomaly Detection through Global Scoring and Calibrated Thresholding

With the widespread availability of sensor data across industrial and operational systems, we frequently encounter heterogeneous time series from multiple systems. Anomaly detection is crucial for such systems to facilitate predictive maintenance. However, most existing anomaly detection methods are designed for either univariate or single-system multivariate data, making them insufficient for these complex scenarios. To address this, we introduce M$^2$AD, a framework for unsupervised anomaly detection in multivariate time series data from multiple systems. M$^2$AD employs deep models to capture expected behavior under normal conditions, using the residuals as indicators of potential anomalies. These residuals are then aggregated into a global anomaly score through a Gaussian Mixture Model and Gamma calibration. We theoretically demonstrate that this framework can effectively address heterogeneity and dependencies across sensors and systems. Empirically, M$^2$AD outperforms existing methods in extensive evaluations by 21% on average, and its effectiveness is demonstrated on a large-scale real-world case study on 130 assets in Amazon Fulfillment Centers. Our code and results are available at https://github.com/sarahmish/M2AD.

Model-Robust and Adaptive-Optimal Transfer Learning for Tackling Concept Shifts in Nonparametric Regression

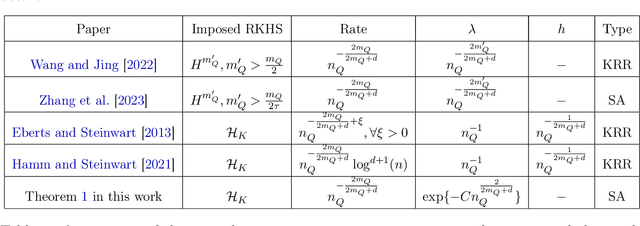
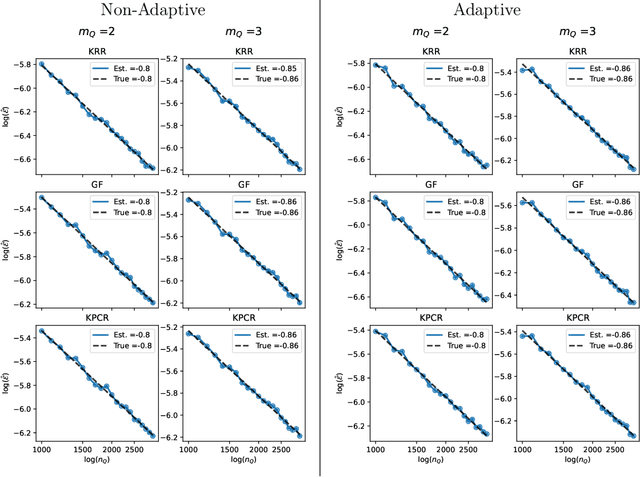
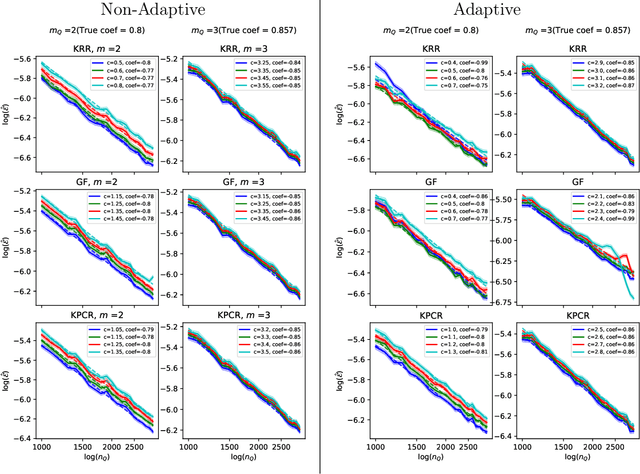
When concept shifts and sample scarcity are present in the target domain of interest, nonparametric regression learners often struggle to generalize effectively. The technique of transfer learning remedies these issues by leveraging data or pre-trained models from similar source domains. While existing generalization analyses of kernel-based transfer learning typically rely on correctly specified models, we present a transfer learning procedure that is robust against model misspecification while adaptively attaining optimality. To facilitate our analysis and avoid the risk of saturation found in classical misspecified results, we establish a novel result in the misspecified single-task learning setting, showing that spectral algorithms with fixed bandwidth Gaussian kernels can attain minimax convergence rates given the true function is in a Sobolev space, which may be of independent interest. Building on this, we derive the adaptive convergence rates of the excess risk for specifying Gaussian kernels in a prevalent class of hypothesis transfer learning algorithms. Our results are minimax optimal up to logarithmic factors and elucidate the key determinants of transfer efficiency.

Smoothness Adaptive Hypothesis Transfer Learning

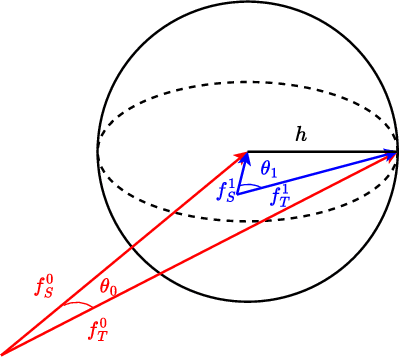
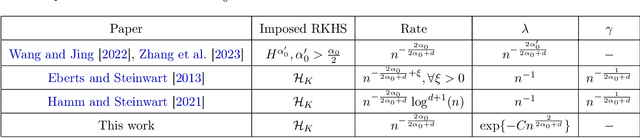
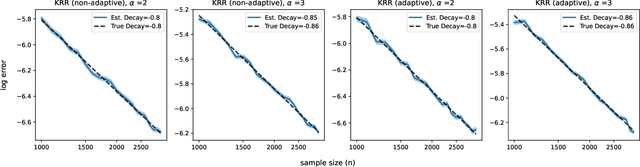
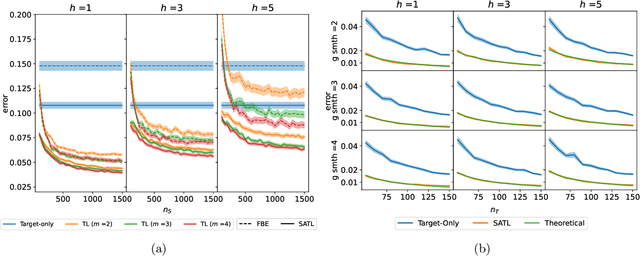
Many existing two-phase kernel-based hypothesis transfer learning algorithms employ the same kernel regularization across phases and rely on the known smoothness of functions to obtain optimality. Therefore, they fail to adapt to the varying and unknown smoothness between the target/source and their offset in practice. In this paper, we address these problems by proposing Smoothness Adaptive Transfer Learning (SATL), a two-phase kernel ridge regression(KRR)-based algorithm. We first prove that employing the misspecified fixed bandwidth Gaussian kernel in target-only KRR learning can achieve minimax optimality and derive an adaptive procedure to the unknown Sobolev smoothness. Leveraging these results, SATL employs Gaussian kernels in both phases so that the estimators can adapt to the unknown smoothness of the target/source and their offset function. We derive the minimax lower bound of the learning problem in excess risk and show that SATL enjoys a matching upper bound up to a logarithmic factor. The minimax convergence rate sheds light on the factors influencing transfer dynamics and demonstrates the superiority of SATL compared to non-transfer learning settings. While our main objective is a theoretical analysis, we also conduct several experiments to confirm our results.

Differentially Private Functional Summaries via the Independent Component Laplace Process

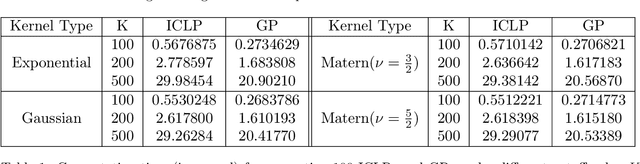
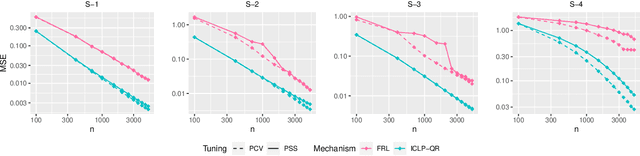
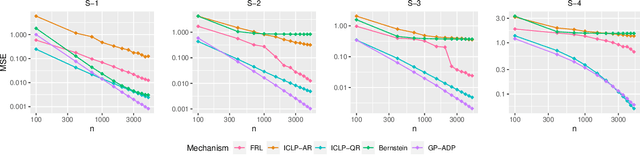
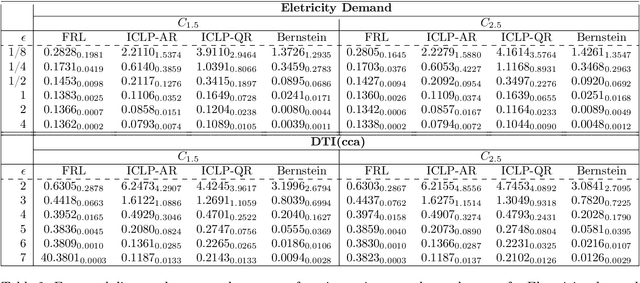
In this work, we propose a new mechanism for releasing differentially private functional summaries called the Independent Component Laplace Process, or ICLP, mechanism. By treating the functional summaries of interest as truly infinite-dimensional objects and perturbing them with the ICLP noise, this new mechanism relaxes assumptions on data trajectories and preserves higher utility compared to classical finite-dimensional subspace embedding approaches in the literature. We establish the feasibility of the proposed mechanism in multiple function spaces. Several statistical estimation problems are considered, and we demonstrate by slightly over-smoothing the summary, the privacy cost will not dominate the statistical error and is asymptotically negligible. Numerical experiments on synthetic and real datasets demonstrate the efficacy of the proposed mechanism.

FAStEN: an efficient adaptive method for feature selection and estimation in high-dimensional functional regressions

Functional regression analysis is an established tool for many contemporary scientific applications. Regression problems involving large and complex data sets are ubiquitous, and feature selection is crucial for avoiding overfitting and achieving accurate predictions. We propose a new, flexible, and ultra-efficient approach to perform feature selection in a sparse high dimensional function-on-function regression problem, and we show how to extend it to the scalar-on-function framework. Our method combines functional data, optimization, and machine learning techniques to perform feature selection and parameter estimation simultaneously. We exploit the properties of Functional Principal Components, and the sparsity inherent to the Dual Augmented Lagrangian problem to significantly reduce computational cost, and we introduce an adaptive scheme to improve selection accuracy. Through an extensive simulation study, we benchmark our approach to the best existing competitors and demonstrate a massive gain in terms of CPU time and selection performance without sacrificing the quality of the coefficients' estimation. Finally, we present an application to brain fMRI data from the AOMIC PIOP1 study.

Shape And Structure Preserving Differential Privacy

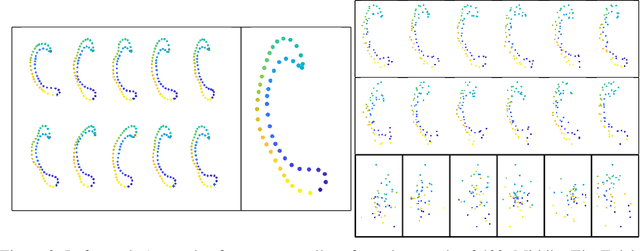
It is common for data structures such as images and shapes of 2D objects to be represented as points on a manifold. The utility of a mechanism to produce sanitized differentially private estimates from such data is intimately linked to how compatible it is with the underlying structure and geometry of the space. In particular, as recently shown, utility of the Laplace mechanism on a positively curved manifold, such as Kendall's 2D shape space, is significantly influences by the curvature. Focusing on the problem of sanitizing the Fr\'echet mean of a sample of points on a manifold, we exploit the characterisation of the mean as the minimizer of an objective function comprised of the sum of squared distances and develop a K-norm gradient mechanism on Riemannian manifolds that favors values that produce gradients close to the the zero of the objective function. For the case of positively curved manifolds, we describe how using the gradient of the squared distance function offers better control over sensitivity than the Laplace mechanism, and demonstrate this numerically on a dataset of shapes of corpus callosa. Further illustrations of the mechanism's utility on a sphere and the manifold of symmetric positive definite matrices are also presented.

On Transfer Learning in Functional Linear Regression

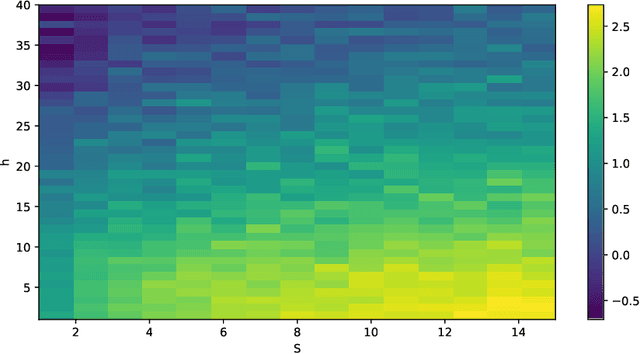
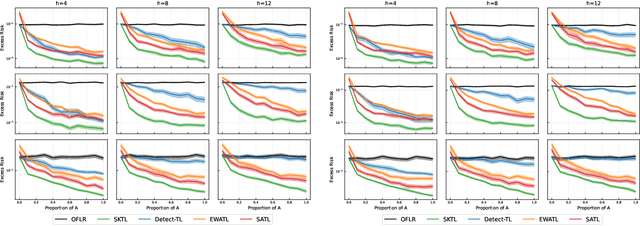
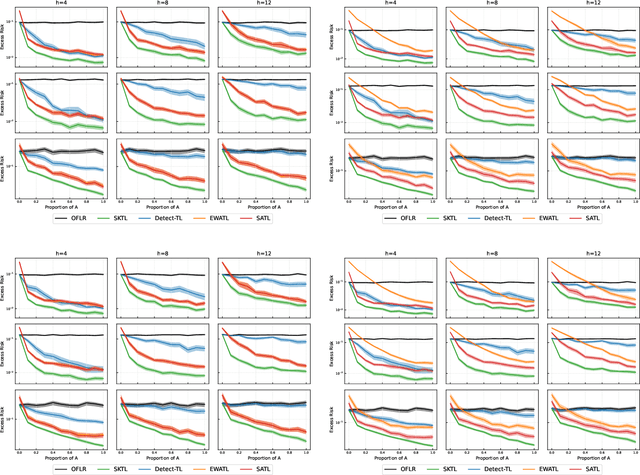
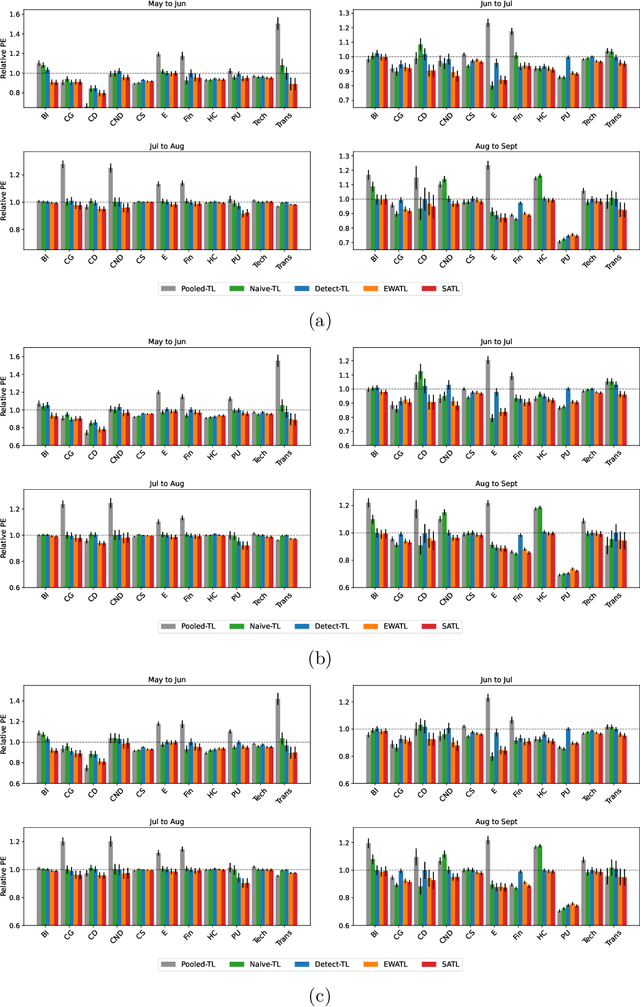
This work studies the problem of transfer learning under the functional linear model framework, which aims to improve the fit of the target model by leveraging the knowledge from related source models. We measure the relatedness between target and source models using Reproducing Kernel Hilbert Spaces, allowing the type of knowledge being transferred to be interpreted by the structure of the spaces. Two algorithms are proposed: one transfers knowledge when the index of transferable sources is known, while the other one utilizes aggregation to achieve knowledge transfer without prior information about the sources. Furthermore, we establish the optimal convergence rates for excess risk, making the statistical gain via transfer learning mathematically provable. The effectiveness of the proposed algorithms is demonstrated on synthetic data as well as real financial data.

Differential Privacy Over Riemannian Manifolds

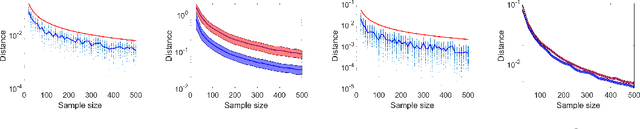
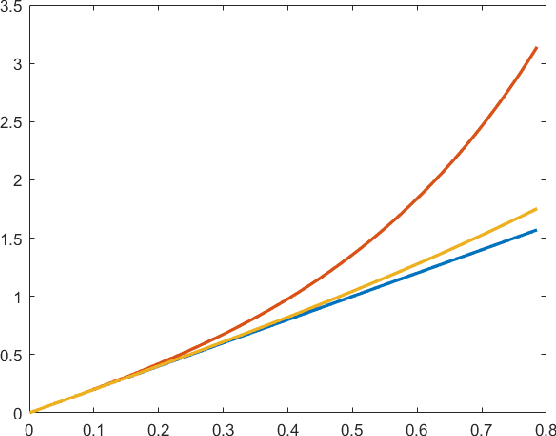
In this work we consider the problem of releasing a differentially private statistical summary that resides on a Riemannian manifold. We present an extension of the Laplace or K-norm mechanism that utilizes intrinsic distances and volumes on the manifold. We also consider in detail the specific case where the summary is the Fr\'echet mean of data residing on a manifold. We demonstrate that our mechanism is rate optimal and depends only on the dimension of the manifold, not on the dimension of any ambient space, while also showing how ignoring the manifold structure can decrease the utility of the sanitized summary. We illustrate our framework in two examples of particular interest in statistics: the space of symmetric positive definite matrices, which is used for covariance matrices, and the sphere, which can be used as a space for modeling discrete distributions.

Modern Non-Linear Function-on-Function Regression

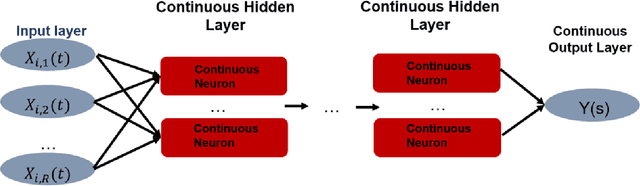
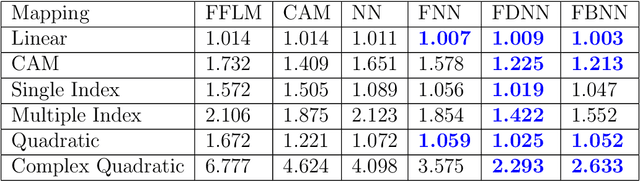
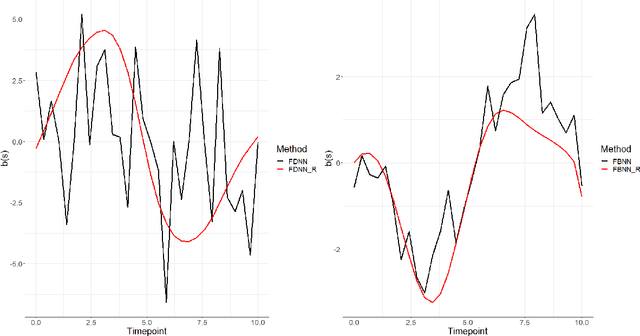
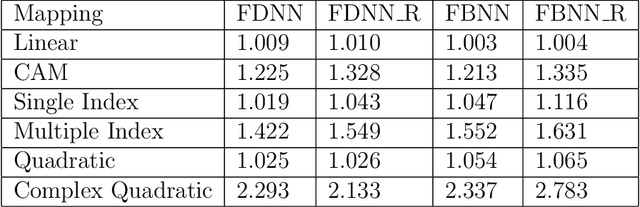
We introduce a new class of non-linear function-on-function regression models for functional data using neural networks. We propose a framework using a hidden layer consisting of continuous neurons, called a continuous hidden layer, for functional response modeling and give two model fitting strategies, Functional Direct Neural Network (FDNN) and Functional Basis Neural Network (FBNN). Both are designed explicitly to exploit the structure inherent in functional data and capture the complex relations existing between the functional predictors and the functional response. We fit these models by deriving functional gradients and implement regularization techniques for more parsimonious results. We demonstrate the power and flexibility of our proposed method in handling complex functional models through extensive simulation studies as well as real data examples.