Functional Graph Convolutional Networks: A unified multi-task and multi-modal learning framework to facilitate health and social-care insights

This paper introduces a novel Functional Graph Convolutional Network (funGCN) framework that combines Functional Data Analysis and Graph Convolutional Networks to address the complexities of multi-task and multi-modal learning in digital health and longitudinal studies. With the growing importance of health solutions to improve health care and social support, ensure healthy lives, and promote well-being at all ages, funGCN offers a unified approach to handle multivariate longitudinal data for multiple entities and ensures interpretability even with small sample sizes. Key innovations include task-specific embedding components that manage different data types, the ability to perform classification, regression, and forecasting, and the creation of a knowledge graph for insightful data interpretation. The efficacy of funGCN is validated through simulation experiments and a real-data application.

Feature Selection for Functional Data Classification

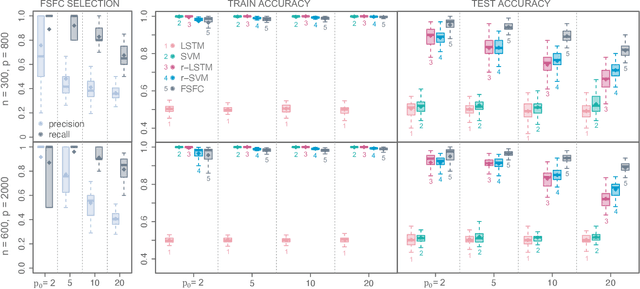
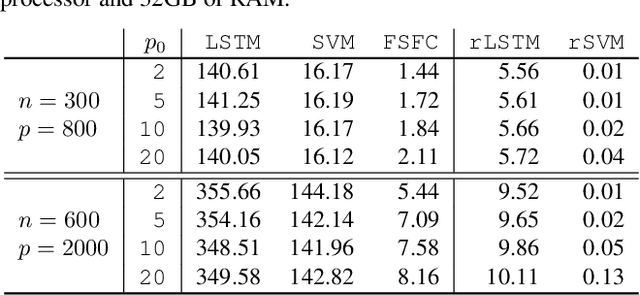
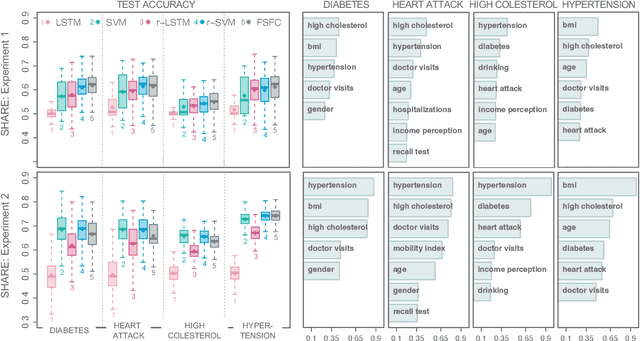
Functional data analysis has emerged as a crucial tool in many contemporary scientific domains that require the integration and interpretation of complex data. Moreover, the advent of new technologies has facilitated the collection of a large number of longitudinal variables, making feature selection pivotal for avoiding overfitting and improving prediction performance. This paper introduces a novel methodology called FSFC (Feature Selection for Functional Classification), that addresses the challenge of jointly performing feature selection and classification of functional data in scenarios with categorical responses and longitudinal features. Our approach tackles a newly defined optimization problem that integrates logistic loss and functional features to identify the most crucial features for classification. To address the minimization procedure, we employ functional principal components and develop a new adaptive version of the Dual Augmented Lagrangian algorithm that leverages the sparsity structure of the problem for dimensionality reduction. The computational efficiency of FSFC enables handling high-dimensional scenarios where the number of features may considerably exceed the number of statistical units. Simulation experiments demonstrate that FSFC outperforms other machine learning and deep learning methods in computational time and classification accuracy. Furthermore, the FSFC feature selection capability can be leveraged to significantly reduce the problem's dimensionality and enhance the performances of other classification algorithms. The efficacy of FSFC is also demonstrated through a real data application, analyzing relationships between four chronic diseases and other health and socio-demographic factors.

FAStEN: an efficient adaptive method for feature selection and estimation in high-dimensional functional regressions

Functional regression analysis is an established tool for many contemporary scientific applications. Regression problems involving large and complex data sets are ubiquitous, and feature selection is crucial for avoiding overfitting and achieving accurate predictions. We propose a new, flexible, and ultra-efficient approach to perform feature selection in a sparse high dimensional function-on-function regression problem, and we show how to extend it to the scalar-on-function framework. Our method combines functional data, optimization, and machine learning techniques to perform feature selection and parameter estimation simultaneously. We exploit the properties of Functional Principal Components, and the sparsity inherent to the Dual Augmented Lagrangian problem to significantly reduce computational cost, and we introduce an adaptive scheme to improve selection accuracy. Through an extensive simulation study, we benchmark our approach to the best existing competitors and demonstrate a massive gain in terms of CPU time and selection performance without sacrificing the quality of the coefficients' estimation. Finally, we present an application to brain fMRI data from the AOMIC PIOP1 study.

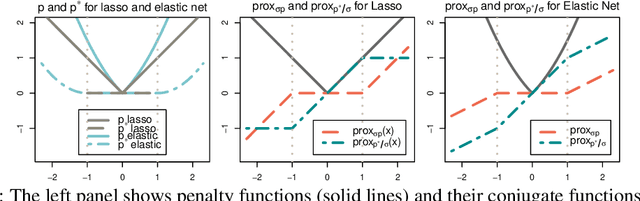
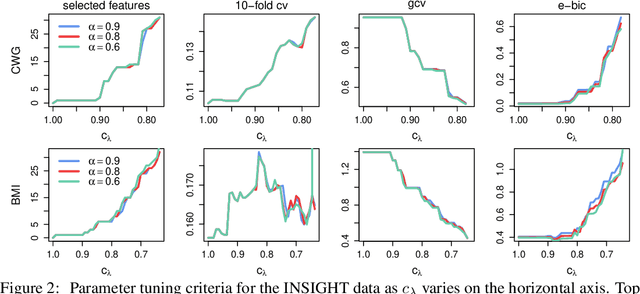
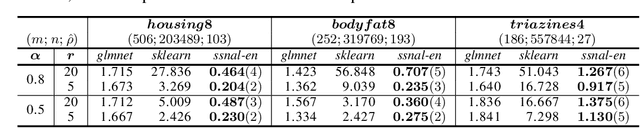
An Efficient Semi-smooth Newton Augmented Lagrangian Method for Elastic Net

Feature selection is an important and active research area in statistics and machine learning. The Elastic Net is often used to perform selection when the features present non-negligible collinearity or practitioners wish to incorporate additional known structure. In this article, we propose a new Semi-smooth Newton Augmented Lagrangian Method to efficiently solve the Elastic Net in ultra-high dimensional settings. Our new algorithm exploits both the sparsity induced by the Elastic Net penalty and the sparsity due to the second order information of the augmented Lagrangian. This greatly reduces the computational cost of the problem. Using simulations on both synthetic and real datasets, we demonstrate that our approach outperforms its best competitors by at least an order of magnitude in terms of CPU time. We also apply our approach to a Genome Wide Association Study on childhood obesity.