Accurate and fast anomaly detection in industrial processes and IoT environments

We present a novel, simple and widely applicable semi-supervised procedure for anomaly detection in industrial and IoT environments, SAnD (Simple Anomaly Detection). SAnD comprises 5 steps, each leveraging well-known statistical tools, namely; smoothing filters, variance inflation factors, the Mahalanobis distance, threshold selection algorithms and feature importance techniques. To our knowledge, SAnD is the first procedure that integrates these tools to identify anomalies and help decipher their putative causes. We show how each step contributes to tackling technical challenges that practitioners face when detecting anomalies in industrial contexts, where signals can be highly multicollinear, have unknown distributions, and intertwine short-lived noise with the long(er)-lived actual anomalies. The development of SAnD was motivated by a concrete case study from our industrial partner, which we use here to show its effectiveness. We also evaluate the performance of SAnD by comparing it with a selection of semi-supervised methods on public datasets from the literature on anomaly detection. We conclude that SAnD is effective, broadly applicable, and outperforms existing approaches in both anomaly detection and runtime.

FAStEN: an efficient adaptive method for feature selection and estimation in high-dimensional functional regressions

Functional regression analysis is an established tool for many contemporary scientific applications. Regression problems involving large and complex data sets are ubiquitous, and feature selection is crucial for avoiding overfitting and achieving accurate predictions. We propose a new, flexible, and ultra-efficient approach to perform feature selection in a sparse high dimensional function-on-function regression problem, and we show how to extend it to the scalar-on-function framework. Our method combines functional data, optimization, and machine learning techniques to perform feature selection and parameter estimation simultaneously. We exploit the properties of Functional Principal Components, and the sparsity inherent to the Dual Augmented Lagrangian problem to significantly reduce computational cost, and we introduce an adaptive scheme to improve selection accuracy. Through an extensive simulation study, we benchmark our approach to the best existing competitors and demonstrate a massive gain in terms of CPU time and selection performance without sacrificing the quality of the coefficients' estimation. Finally, we present an application to brain fMRI data from the AOMIC PIOP1 study.

Epsilon Consistent Mixup: An Adaptive Consistency-Interpolation Tradeoff

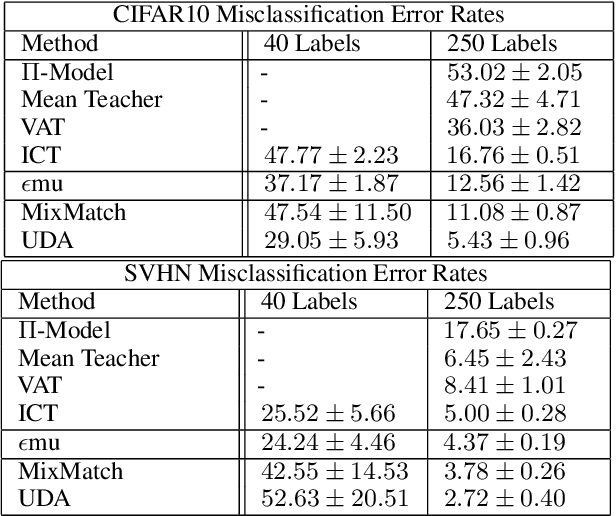
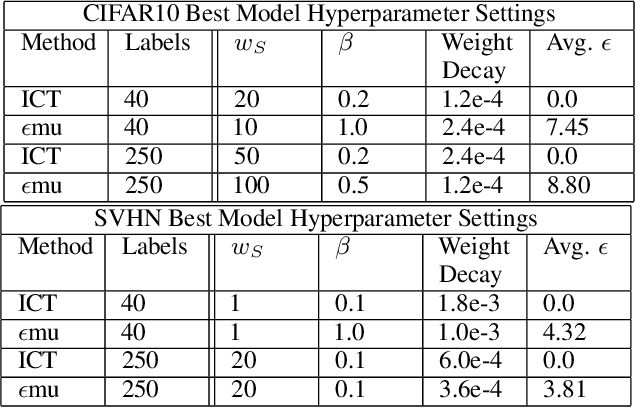
In this paper we propose $\epsilon$-Consistent Mixup ($\epsilon$mu). $\epsilon$mu is a data-based structural regularization technique that combines Mixup's linear interpolation with consistency regularization in the Mixup direction, by compelling a simple adaptive tradeoff between the two. This learnable combination of consistency and interpolation induces a more flexible structure on the evolution of the response across the feature space and is shown to improve semi-supervised classification accuracy on the SVHN and CIFAR10 benchmark datasets, yielding the largest gains in the most challenging low label-availability scenarios. Empirical studies comparing $\epsilon$mu and Mixup are presented and provide insight into the mechanisms behind $\epsilon$mu's effectiveness. In particular, $\epsilon$mu is found to produce more accurate synthetic labels and more confident predictions than Mixup.

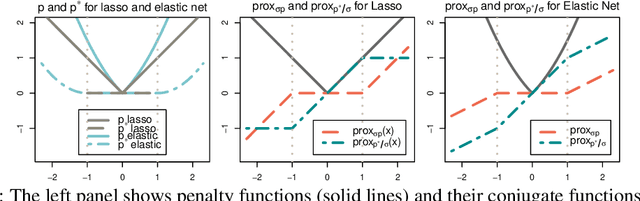
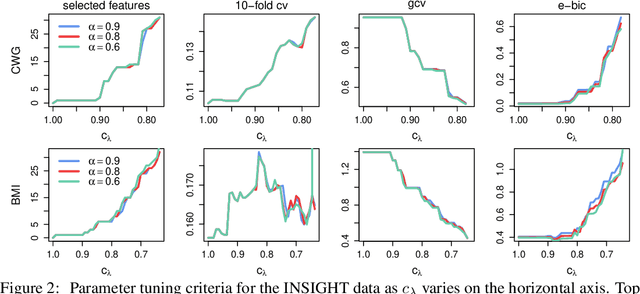
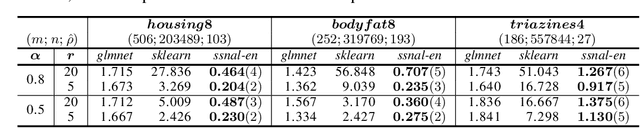
An Efficient Semi-smooth Newton Augmented Lagrangian Method for Elastic Net

Feature selection is an important and active research area in statistics and machine learning. The Elastic Net is often used to perform selection when the features present non-negligible collinearity or practitioners wish to incorporate additional known structure. In this article, we propose a new Semi-smooth Newton Augmented Lagrangian Method to efficiently solve the Elastic Net in ultra-high dimensional settings. Our new algorithm exploits both the sparsity induced by the Elastic Net penalty and the sparsity due to the second order information of the augmented Lagrangian. This greatly reduces the computational cost of the problem. Using simulations on both synthetic and real datasets, we demonstrate that our approach outperforms its best competitors by at least an order of magnitude in terms of CPU time. We also apply our approach to a Genome Wide Association Study on childhood obesity.

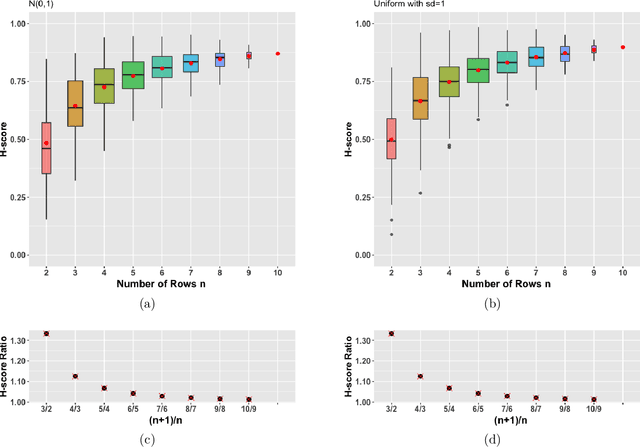
On the bias of H-scores for comparing biclusters, and how to correct it

In the last two decades several biclustering methods have been developed as new unsupervised learning techniques to simultaneously cluster rows and columns of a data matrix. These algorithms play a central role in contemporary machine learning and in many applications, e.g. to computational biology and bioinformatics. The H-score is the evaluation score underlying the seminal biclustering algorithm by Cheng and Church, as well as many other subsequent biclustering methods. In this paper, we characterize a potentially troublesome bias in this score, that can distort biclustering results. We prove, both analytically and by simulation, that the average H-score increases with the number of rows/columns in a bicluster. This makes the H-score, and hence all algorithms based on it, biased towards small clusters. Based on our analytical proof, we are able to provide a straightforward way to correct this bias, allowing users to accurately compare biclusters.

Linear Contour Learning: A Method for Supervised Dimension Reduction

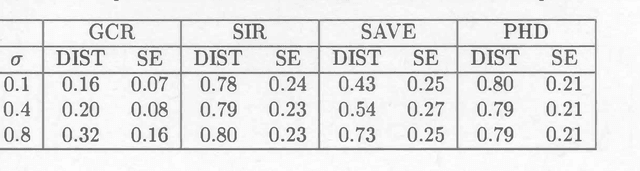
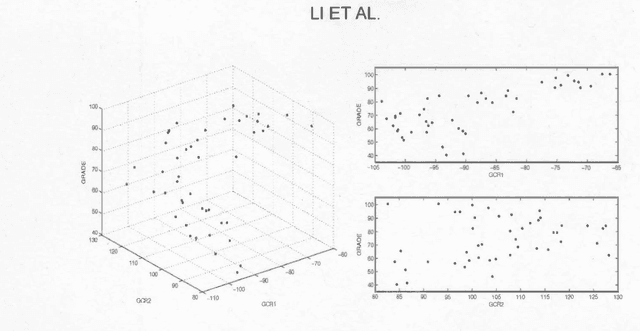
We propose a novel approach to sufficient dimension reduction in regression, based on estimating contour directions of negligible variation for the response surface. These directions span the orthogonal complement of the minimal space relevant for the regression, and can be extracted according to a measure of the variation in the response, leading to General Contour Regression(GCR). In comparison to exiisting sufficient dimension reduction techniques, this sontour-based mothology guarantees exhaustive estimation of the central space under ellipticity of the predictoor distribution and very mild additional assumptions, while maintaining vn-consisytency and somputational ease. Moreover, it proves to be robust to departures from ellipticity. We also establish some useful population properties for GCR. Simulations to compare performance with that of standard techniques such as ordinary least squares, sliced inverse regression, principal hessian directions, and sliced average variance estimation confirm the advntages anticipated by theoretical analyses. We also demonstrate the use of contour-based methods on a data set concerning grades of students from Massachusetts colleges.