Epsilon Consistent Mixup: An Adaptive Consistency-Interpolation Tradeoff
Paper and Code
Apr 19, 2021
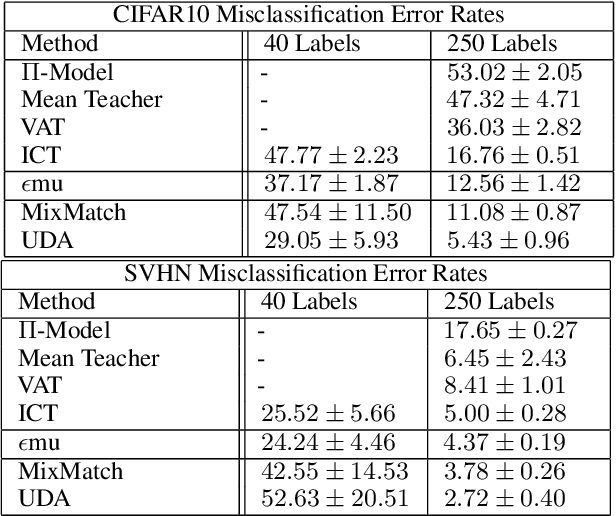

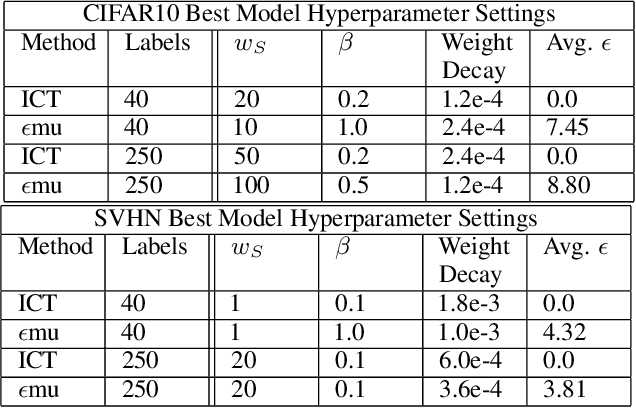
In this paper we propose $\epsilon$-Consistent Mixup ($\epsilon$mu). $\epsilon$mu is a data-based structural regularization technique that combines Mixup's linear interpolation with consistency regularization in the Mixup direction, by compelling a simple adaptive tradeoff between the two. This learnable combination of consistency and interpolation induces a more flexible structure on the evolution of the response across the feature space and is shown to improve semi-supervised classification accuracy on the SVHN and CIFAR10 benchmark datasets, yielding the largest gains in the most challenging low label-availability scenarios. Empirical studies comparing $\epsilon$mu and Mixup are presented and provide insight into the mechanisms behind $\epsilon$mu's effectiveness. In particular, $\epsilon$mu is found to produce more accurate synthetic labels and more confident predictions than Mixup.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge