On the bias of H-scores for comparing biclusters, and how to correct it

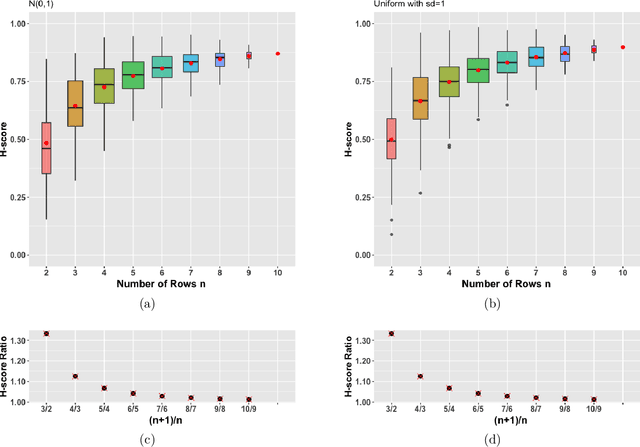
In the last two decades several biclustering methods have been developed as new unsupervised learning techniques to simultaneously cluster rows and columns of a data matrix. These algorithms play a central role in contemporary machine learning and in many applications, e.g. to computational biology and bioinformatics. The H-score is the evaluation score underlying the seminal biclustering algorithm by Cheng and Church, as well as many other subsequent biclustering methods. In this paper, we characterize a potentially troublesome bias in this score, that can distort biclustering results. We prove, both analytically and by simulation, that the average H-score increases with the number of rows/columns in a bicluster. This makes the H-score, and hence all algorithms based on it, biased towards small clusters. Based on our analytical proof, we are able to provide a straightforward way to correct this bias, allowing users to accurately compare biclusters.