Linear Contour Learning: A Method for Supervised Dimension Reduction
Paper and Code
Aug 13, 2014
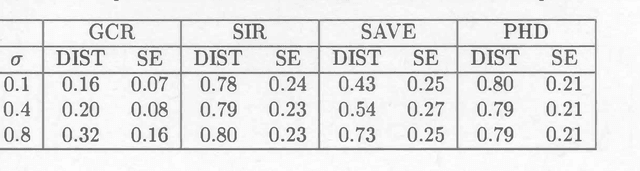

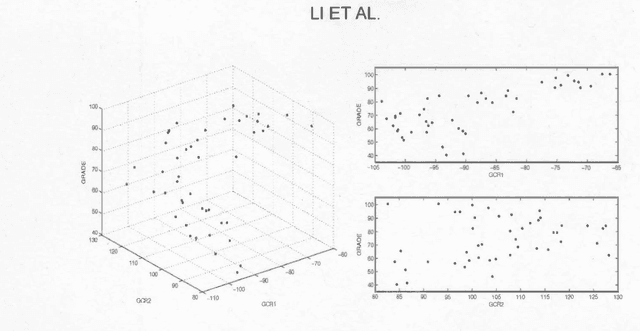
We propose a novel approach to sufficient dimension reduction in regression, based on estimating contour directions of negligible variation for the response surface. These directions span the orthogonal complement of the minimal space relevant for the regression, and can be extracted according to a measure of the variation in the response, leading to General Contour Regression(GCR). In comparison to exiisting sufficient dimension reduction techniques, this sontour-based mothology guarantees exhaustive estimation of the central space under ellipticity of the predictoor distribution and very mild additional assumptions, while maintaining vn-consisytency and somputational ease. Moreover, it proves to be robust to departures from ellipticity. We also establish some useful population properties for GCR. Simulations to compare performance with that of standard techniques such as ordinary least squares, sliced inverse regression, principal hessian directions, and sliced average variance estimation confirm the advntages anticipated by theoretical analyses. We also demonstrate the use of contour-based methods on a data set concerning grades of students from Massachusetts colleges.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge