An Efficient Semi-smooth Newton Augmented Lagrangian Method for Elastic Net
Paper and Code
Jun 06, 2020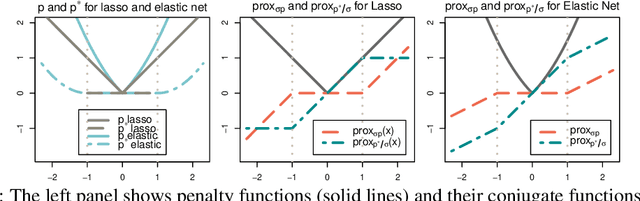

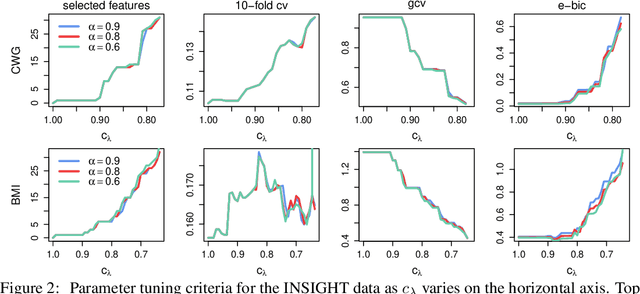
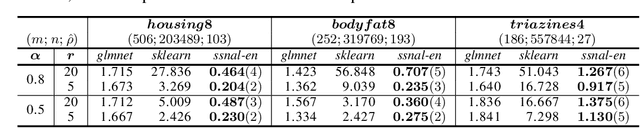
Feature selection is an important and active research area in statistics and machine learning. The Elastic Net is often used to perform selection when the features present non-negligible collinearity or practitioners wish to incorporate additional known structure. In this article, we propose a new Semi-smooth Newton Augmented Lagrangian Method to efficiently solve the Elastic Net in ultra-high dimensional settings. Our new algorithm exploits both the sparsity induced by the Elastic Net penalty and the sparsity due to the second order information of the augmented Lagrangian. This greatly reduces the computational cost of the problem. Using simulations on both synthetic and real datasets, we demonstrate that our approach outperforms its best competitors by at least an order of magnitude in terms of CPU time. We also apply our approach to a Genome Wide Association Study on childhood obesity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge