Equipment Health Assessment: Time Series Analysis for Wind Turbine Performance

In this study, we leverage SCADA data from diverse wind turbines to predict power output, employing advanced time series methods, specifically Functional Neural Networks (FNN) and Long Short-Term Memory (LSTM) networks. A key innovation lies in the ensemble of FNN and LSTM models, capitalizing on their collective learning. This ensemble approach outperforms individual models, ensuring stable and accurate power output predictions. Additionally, machine learning techniques are applied to detect wind turbine performance deterioration, enabling proactive maintenance strategies and health assessment. Crucially, our analysis reveals the uniqueness of each wind turbine, necessitating tailored models for optimal predictions. These insight underscores the importance of providing automatized customization for different turbines to keep human modeling effort low. Importantly, the methodologies developed in this analysis are not limited to wind turbines; they can be extended to predict and optimize performance in various machinery, highlighting the versatility and applicability of our research across diverse industrial contexts.

Predictive Analysis for Optimizing Port Operations

Maritime transport is a pivotal logistics mode for the long-distance and bulk transportation of goods. However, the intricate planning involved in this mode is often hindered by uncertainties, including weather conditions, cargo diversity, and port dynamics, leading to increased costs. Consequently, accurately estimating vessel total (stay) time at port and potential delays becomes imperative for effective planning and scheduling in port operations. This study aims to develop a port operation solution with competitive prediction and classification capabilities for estimating vessel Total and Delay times. This research addresses a significant gap in port analysis models for vessel Stay and Delay times, offering a valuable contribution to the field of maritime logistics. The proposed solution is designed to assist decision-making in port environments and predict service delays. This is demonstrated through a case study on Brazil ports. Additionally, feature analysis is used to understand the key factors impacting maritime logistics, enhancing the overall understanding of the complexities involved in port operations.

An ensemble of convolution-based methods for fault detection using vibration signals

This paper focuses on solving a fault detection problem using multivariate time series of vibration signals collected from planetary gearboxes in a test rig. Various traditional machine learning and deep learning methods have been proposed for multivariate time-series classification, including distance-based, functional data-oriented, feature-driven, and convolution kernel-based methods. Recent studies have shown using convolution kernel-based methods like ROCKET, and 1D convolutional neural networks with ResNet and FCN, have robust performance for multivariate time-series data classification. We propose an ensemble of three convolution kernel-based methods and show its efficacy on this fault detection problem by outperforming other approaches and achieving an accuracy of more than 98.8\%.

A Functional approach for Two Way Dimension Reduction in Time Series

The rise in data has led to the need for dimension reduction techniques, especially in the area of non-scalar variables, including time series, natural language processing, and computer vision. In this paper, we specifically investigate dimension reduction for time series through functional data analysis. Current methods for dimension reduction in functional data are functional principal component analysis and functional autoencoders, which are limited to linear mappings or scalar representations for the time series, which is inefficient. In real data applications, the nature of the data is much more complex. We propose a non-linear function-on-function approach, which consists of a functional encoder and a functional decoder, that uses continuous hidden layers consisting of continuous neurons to learn the structure inherent in functional data, which addresses the aforementioned concerns in the existing approaches. Our approach gives a low dimension latent representation by reducing the number of functional features as well as the timepoints at which the functions are observed. The effectiveness of the proposed model is demonstrated through multiple simulations and real data examples.

Modern Non-Linear Function-on-Function Regression

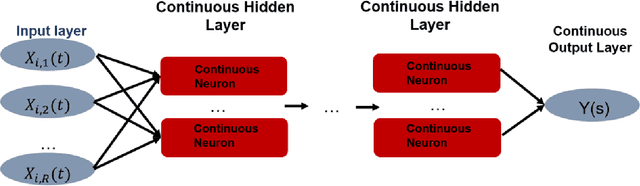
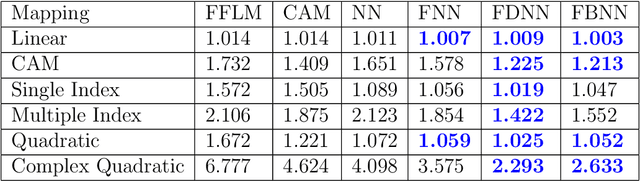
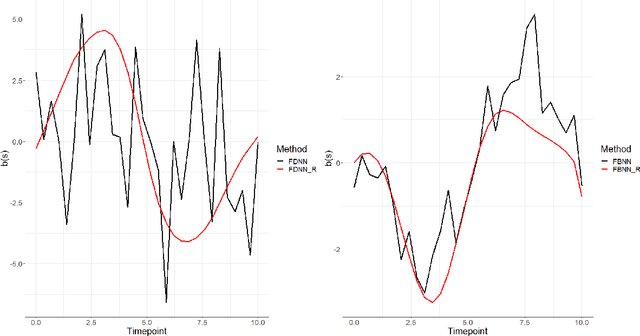
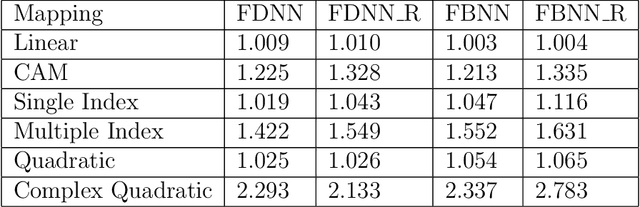
We introduce a new class of non-linear function-on-function regression models for functional data using neural networks. We propose a framework using a hidden layer consisting of continuous neurons, called a continuous hidden layer, for functional response modeling and give two model fitting strategies, Functional Direct Neural Network (FDNN) and Functional Basis Neural Network (FBNN). Both are designed explicitly to exploit the structure inherent in functional data and capture the complex relations existing between the functional predictors and the functional response. We fit these models by deriving functional gradients and implement regularization techniques for more parsimonious results. We demonstrate the power and flexibility of our proposed method in handling complex functional models through extensive simulation studies as well as real data examples.

Non-linear Functional Modeling using Neural Networks

We introduce a new class of non-linear models for functional data based on neural networks. Deep learning has been very successful in non-linear modeling, but there has been little work done in the functional data setting. We propose two variations of our framework: a functional neural network with continuous hidden layers, called the Functional Direct Neural Network (FDNN), and a second version that utilizes basis expansions and continuous hidden layers, called the Functional Basis Neural Network (FBNN). Both are designed explicitly to exploit the structure inherent in functional data. To fit these models we derive a functional gradient based optimization algorithm. The effectiveness of the proposed methods in handling complex functional models is demonstrated by comprehensive simulation studies and real data examples.

Modern Multiple Imputation with Functional Data

This work considers the problem of fitting functional models with sparsely and irregularly sampled functional data. It overcomes the limitations of the state-of-the-art methods, which face major challenges in the fitting of more complex non-linear models. Currently, many of these models cannot be consistently estimated unless the number of observed points per curve grows sufficiently quickly with the sample size, whereas, we show numerically that a modified approach with more modern multiple imputation methods can produce better estimates in general. We also propose a new imputation approach that combines the ideas of {\it MissForest} with {\it Local Linear Forest} and compare their performance with {\it PACE} and several other multivariate multiple imputation methods. This work is motivated by a longitudinal study on smoking cessation, in which the Electronic Health Records (EHR) from Penn State PaTH to Health allow for the collection of a great deal of data, with highly variable sampling. To illustrate our approach, we explore the relation between relapse and diastolic blood pressure. We also consider a variety of simulation schemes with varying levels of sparsity to validate our methods.

A Non-linear Function-on-Function Model for Regression with Time Series Data

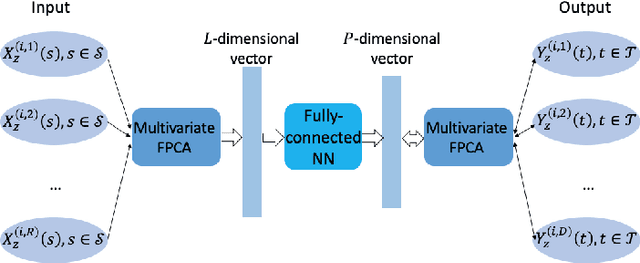
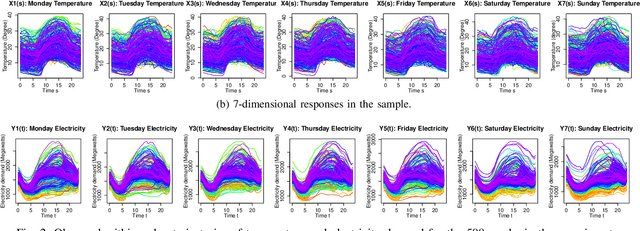
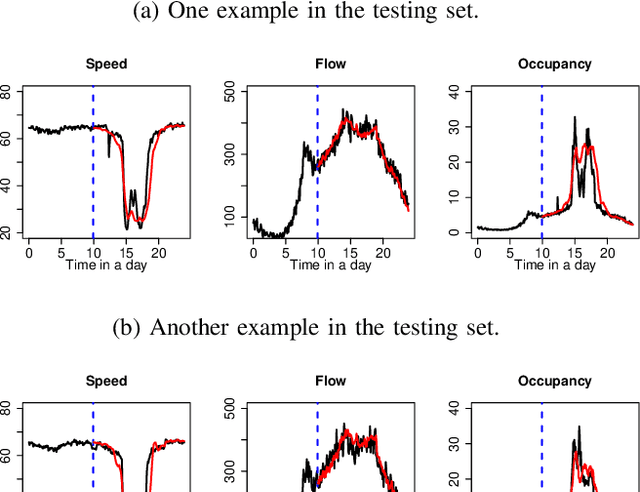
In the last few decades, building regression models for non-scalar variables, including time series, text, image, and video, has attracted increasing interests of researchers from the data analytic community. In this paper, we focus on a multivariate time series regression problem. Specifically, we aim to learn mathematical mappings from multiple chronologically measured numerical variables within a certain time interval S to multiple numerical variables of interest over time interval T. Prior arts, including the multivariate regression model, the Seq2Seq model, and the functional linear models, suffer from several limitations. The first two types of models can only handle regularly observed time series. Besides, the conventional multivariate regression models tend to be biased and inefficient, as they are incapable of encoding the temporal dependencies among observations from the same time series. The sequential learning models explicitly use the same set of parameters along time, which has negative impacts on accuracy. The function-on-function linear model in functional data analysis (a branch of statistics) is insufficient to capture complex correlations among the considered time series and suffer from underfitting easily. In this paper, we propose a general functional mapping that embraces the function-on-function linear model as a special case. We then propose a non-linear function-on-function model using the fully connected neural network to learn the mapping from data, which addresses the aforementioned concerns in the existing approaches. For the proposed model, we describe in detail the corresponding numerical implementation procedures. The effectiveness of the proposed model is demonstrated through the application to two real-world problems.

Spatio-Temporal Functional Neural Networks

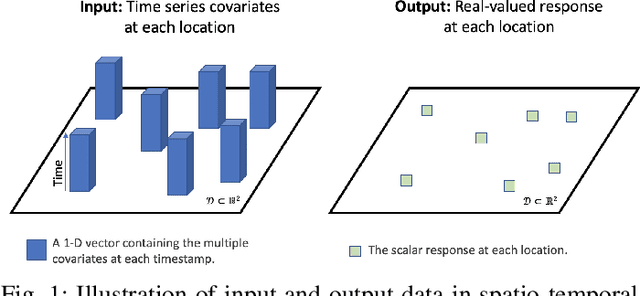
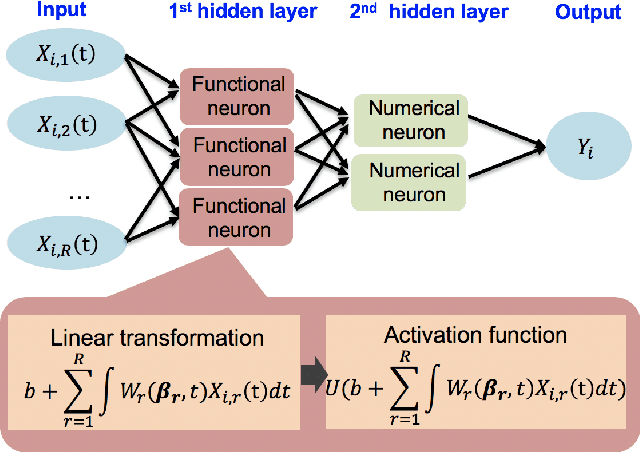
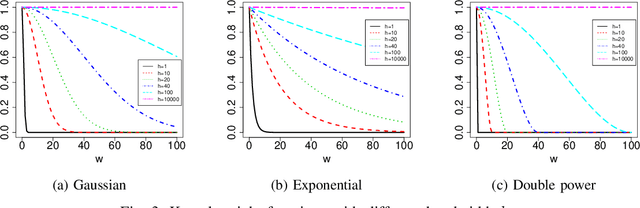
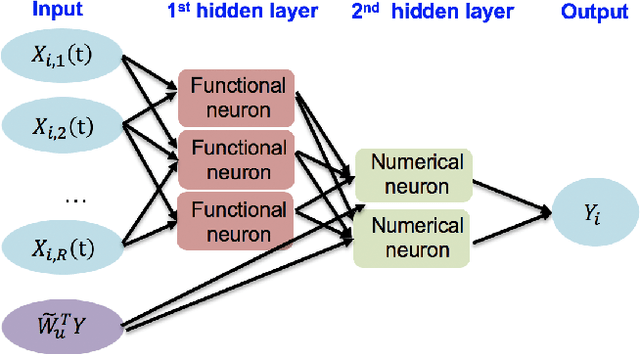
Explosive growth in spatio-temporal data and its wide range of applications have attracted increasing interests of researchers in the statistical and machine learning fields. The spatio-temporal regression problem is of paramount importance from both the methodology development and real-world application perspectives. Given the observed spatially encoded time series covariates and real-valued response data samples, the goal of spatio-temporal regression is to leverage the temporal and spatial dependencies to build a mapping from covariates to response with minimized prediction error. Prior arts, including the convolutional Long Short-Term Memory (CovLSTM) and variations of the functional linear models, cannot learn the spatio-temporal information in a simple and efficient format for proper model building. In this work, we propose two novel extensions of the Functional Neural Network (FNN), a temporal regression model whose effectiveness and superior performance over alternative sequential models have been proven by many researchers. The effectiveness of the proposed spatio-temporal FNNs in handling varying spatial correlations is demonstrated in comprehensive simulation studies. The proposed models are then deployed to solve a practical and challenging precipitation prediction problem in the meteorology field.