A Functional approach for Two Way Dimension Reduction in Time Series
Paper and Code
Jan 01, 2023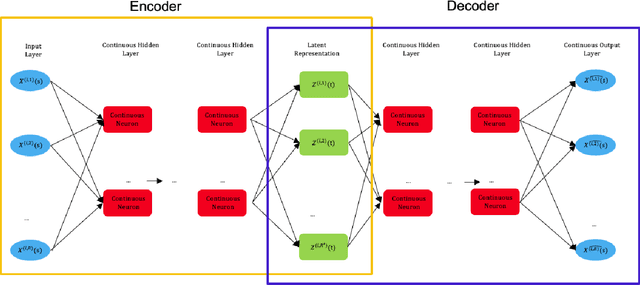
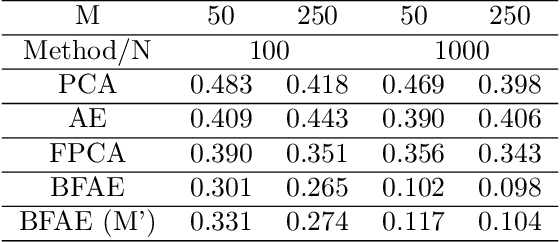
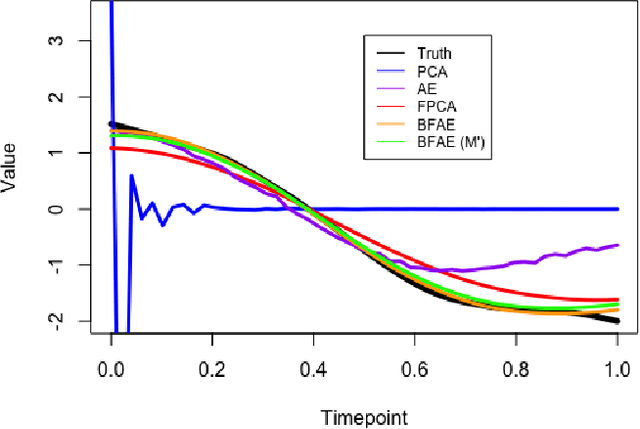
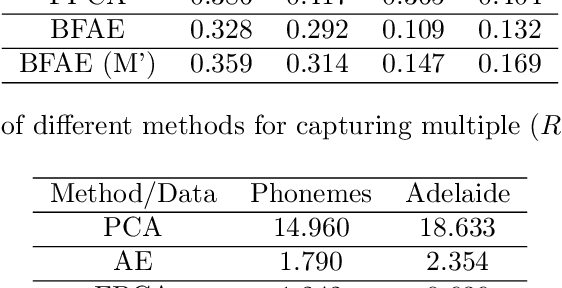
The rise in data has led to the need for dimension reduction techniques, especially in the area of non-scalar variables, including time series, natural language processing, and computer vision. In this paper, we specifically investigate dimension reduction for time series through functional data analysis. Current methods for dimension reduction in functional data are functional principal component analysis and functional autoencoders, which are limited to linear mappings or scalar representations for the time series, which is inefficient. In real data applications, the nature of the data is much more complex. We propose a non-linear function-on-function approach, which consists of a functional encoder and a functional decoder, that uses continuous hidden layers consisting of continuous neurons to learn the structure inherent in functional data, which addresses the aforementioned concerns in the existing approaches. Our approach gives a low dimension latent representation by reducing the number of functional features as well as the timepoints at which the functions are observed. The effectiveness of the proposed model is demonstrated through multiple simulations and real data examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge