Smoothness Adaptive Hypothesis Transfer Learning
Paper and Code
Feb 22, 2024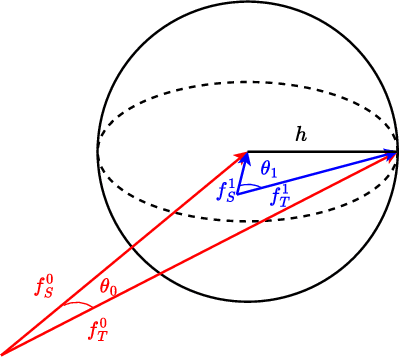
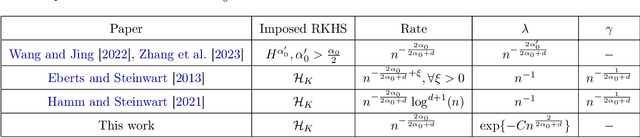
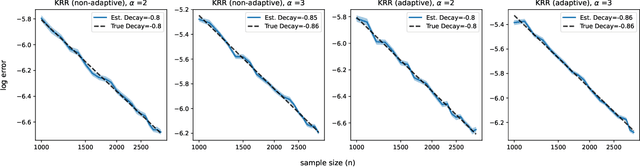
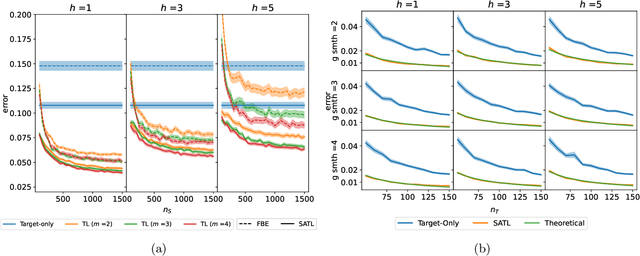
Many existing two-phase kernel-based hypothesis transfer learning algorithms employ the same kernel regularization across phases and rely on the known smoothness of functions to obtain optimality. Therefore, they fail to adapt to the varying and unknown smoothness between the target/source and their offset in practice. In this paper, we address these problems by proposing Smoothness Adaptive Transfer Learning (SATL), a two-phase kernel ridge regression(KRR)-based algorithm. We first prove that employing the misspecified fixed bandwidth Gaussian kernel in target-only KRR learning can achieve minimax optimality and derive an adaptive procedure to the unknown Sobolev smoothness. Leveraging these results, SATL employs Gaussian kernels in both phases so that the estimators can adapt to the unknown smoothness of the target/source and their offset function. We derive the minimax lower bound of the learning problem in excess risk and show that SATL enjoys a matching upper bound up to a logarithmic factor. The minimax convergence rate sheds light on the factors influencing transfer dynamics and demonstrates the superiority of SATL compared to non-transfer learning settings. While our main objective is a theoretical analysis, we also conduct several experiments to confirm our results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge