Learning in structured MDPs with convex cost functions: Improved regret bounds for inventory management
Paper and Code
May 10, 2019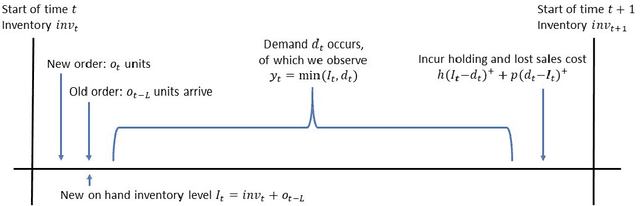
We consider a stochastic inventory control problem under censored demands, lost sales, and positive lead times. This is a fundamental problem in inventory management, with significant literature establishing near-optimality of a simple class of policies called ``base-stock policies'' for the underlying Markov Decision Process (MDP), as well as convexity of long run average-cost under those policies. We consider the relatively less studied problem of designing a learning algorithm for this problem when the underlying demand distribution is unknown. The goal is to bound regret of the algorithm when compared to the best base-stock policy. We utilize the convexity properties and a newly derived bound on bias of base-stock policies to establish a connection to stochastic convex bandit optimization. Our main contribution is a learning algorithm with a regret bound of $\tilde{O}(L\sqrt{T}+D)$ for the inventory control problem. Here $L$ is the fixed and known lead time, and $D$ is an unknown parameter of the demand distribution described roughly as the number of time steps needed to generate enough demand for depleting one unit of inventory. Notably, even though the state space of the underlying MDP is continuous and $L$-dimensional, our regret bounds depend linearly on $L$. Our results significantly improve the previously best known regret bounds for this problem where the dependence on $L$ was exponential and many further assumptions on demand distribution were required. The techniques presented here may be of independent interest for other settings that involve large structured MDPs but with convex cost functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge