Efficient, Certifiably Optimal Clustering with Applications to Latent Variable Graphical Models

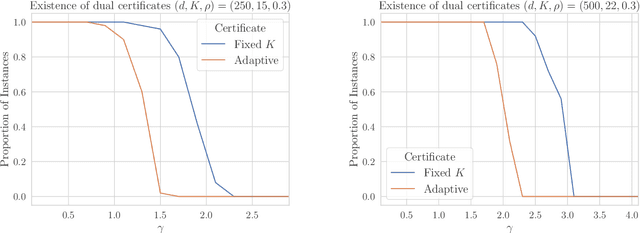
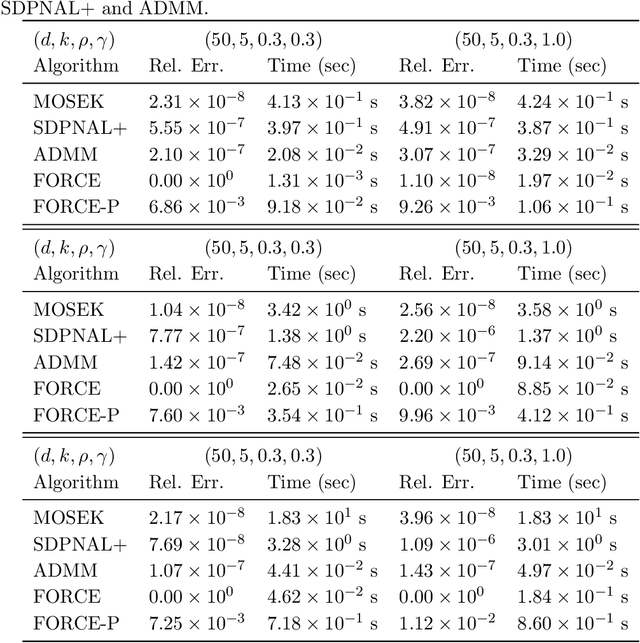
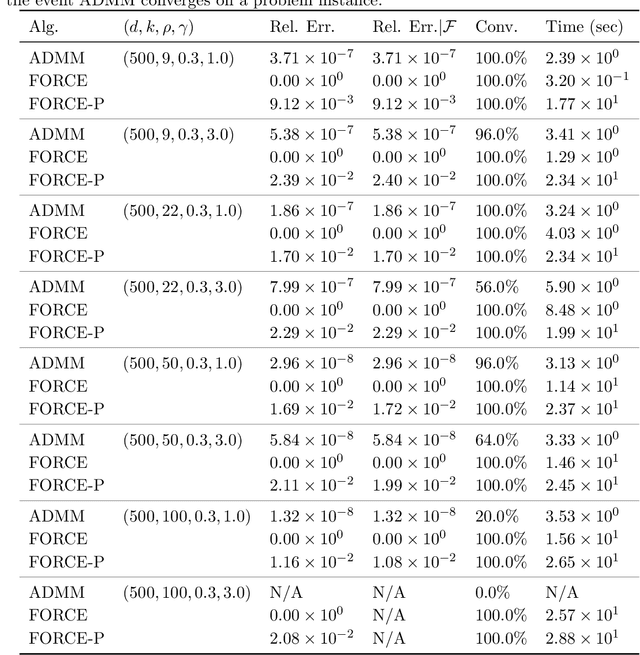
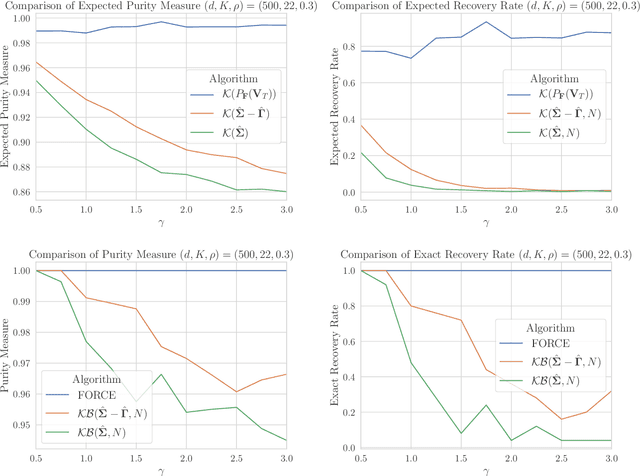
Motivated by the task of clustering either $d$ variables or $d$ points into $K$ groups, we investigate efficient algorithms to solve the Peng-Wei (P-W) $K$-means semi-definite programming (SDP) relaxation. The P-W SDP has been shown in the literature to have good statistical properties in a variety of settings, but remains intractable to solve in practice. To this end we propose FORCE, a new algorithm to solve this SDP relaxation. Compared to the naive interior point method, our method reduces the computational complexity of solving the SDP from $\tilde{O}(d^7\log\epsilon^{-1})$ to $\tilde{O}(d^{6}K^{-2}\epsilon^{-1})$ arithmetic operations for an $\epsilon$-optimal solution. Our method combines a primal first-order method with a dual optimality certificate search, which when successful, allows for early termination of the primal method. We show for certain variable clustering problems that, with high probability, FORCE is guaranteed to find the optimal solution to the SDP relaxation and provide a certificate of exact optimality. As verified by our numerical experiments, this allows FORCE to solve the P-W SDP with dimensions in the hundreds in only tens of seconds. For a variation of the P-W SDP where $K$ is not known a priori a slight modification of FORCE reduces the computational complexity of solving this problem as well: from $\tilde{O}(d^7\log\epsilon^{-1})$ using a standard SDP solver to $\tilde{O}(d^{4}\epsilon^{-1})$.