Generative Reasoning Re-ranker

Recent studies increasingly explore Large Language Models (LLMs) as a new paradigm for recommendation systems due to their scalability and world knowledge. However, existing work has three key limitations: (1) most efforts focus on retrieval and ranking, while the reranking phase, critical for refining final recommendations, is largely overlooked; (2) LLMs are typically used in zero-shot or supervised fine-tuning settings, leaving their reasoning abilities, especially those enhanced through reinforcement learning (RL) and high-quality reasoning data, underexploited; (3) items are commonly represented by non-semantic IDs, creating major scalability challenges in industrial systems with billions of identifiers. To address these gaps, we propose the Generative Reasoning Reranker (GR2), an end-to-end framework with a three-stage training pipeline tailored for reranking. First, a pretrained LLM is mid-trained on semantic IDs encoded from non-semantic IDs via a tokenizer achieving $\ge$99% uniqueness. Next, a stronger larger-scale LLM generates high-quality reasoning traces through carefully designed prompting and rejection sampling, which are used for supervised fine-tuning to impart foundational reasoning skills. Finally, we apply Decoupled Clip and Dynamic sAmpling Policy Optimization (DAPO), enabling scalable RL supervision with verifiable rewards designed specifically for reranking. Experiments on two real-world datasets demonstrate GR2's effectiveness: it surpasses the state-of-the-art OneRec-Think by 2.4% in Recall@5 and 1.3% in NDCG@5. Ablations confirm that advanced reasoning traces yield substantial gains across metrics. We further find that RL reward design is crucial in reranking: LLMs tend to exploit reward hacking by preserving item order, motivating conditional verifiable rewards to mitigate this behavior and optimize reranking performance.

Displacement-Resistant Extensions of DPO with Nonconvex $f$-Divergences

DPO and related algorithms align language models by directly optimizing the RLHF objective: find a policy that maximizes the Bradley-Terry reward while staying close to a reference policy through a KL divergence penalty. Previous work showed that this approach could be further generalized: the original problem remains tractable even if the KL divergence is replaced by a family of $f$-divergence with a convex generating function $f$. Our first contribution is to show that convexity of $f$ is not essential. Instead, we identify a more general condition, referred to as DPO-inducing, that precisely characterizes when the RLHF problem remains tractable. Our next contribution is to establish a second condition on $f$ that is necessary to prevent probability displacement, a known empirical phenomenon in which the probabilities of the winner and the loser responses approach zero. We refer to any $f$ that satisfies this condition as displacement-resistant. We finally focus on a specific DPO-inducing and displacement-resistant $f$, leading to our novel SquaredPO loss. Compared to DPO, this new loss offers stronger theoretical guarantees while performing competitively in practice.

Structure Enables Effective Self-Localization of Errors in LLMs

Self-correction in language models remains elusive. In this work, we explore whether language models can explicitly localize errors in incorrect reasoning, as a path toward building AI systems that can effectively correct themselves. We introduce a prompting method that structures reasoning as discrete, semantically coherent thought steps, and show that models are able to reliably localize errors within this structure, while failing to do so in conventional, unstructured chain-of-thought reasoning. Motivated by how the human brain monitors errors at discrete decision points and resamples alternatives, we introduce Iterative Correction Sampling of Thoughts (Thought-ICS), a self-correction framework. Thought-ICS iteratively prompts the model to generate reasoning one discrete and complete thought at a time--where each thought represents a deliberate decision by the model--creating natural boundaries for precise error localization. Upon verification, the model localizes the first erroneous step, and the system backtracks to generate alternative reasoning from the last correct point. When asked to correct reasoning verified as incorrect by an oracle, Thought-ICS achieves 20-40% self-correction lift. In a completely autonomous setting without external verification, it outperforms contemporary self-correction baselines.

C-3DPO: Constrained Controlled Classification for Direct Preference Optimization

Direct preference optimization (DPO)-style algorithms have emerged as a promising approach for solving the alignment problem in AI. We present a novel perspective that formulates these algorithms as implicit classification algorithms. This classification framework enables us to recover many variants of DPO-style algorithms by choosing appropriate classification labels and loss functions. We then leverage this classification framework to demonstrate that the underlying problem solved in these algorithms is under-specified, making them susceptible to probability collapse of the winner-loser responses. We address this by proposing a set of constraints designed to control the movement of probability mass between the winner and loser in the reference and target policies. Our resulting algorithm, which we call Constrained Controlled Classification DPO (\texttt{C-3DPO}), has a meaningful RLHF interpretation. By hedging against probability collapse, \texttt{C-3DPO} provides practical improvements over vanilla \texttt{DPO} when aligning several large language models using standard preference datasets.

Adjoint sharding for very long context training of state space models

Despite very fast progress, efficiently training large language models (LLMs) in very long contexts remains challenging. Existing methods fall back to training LLMs with short contexts (a maximum of a few thousands tokens in training) and use inference time techniques when evaluating on long contexts (above 1M tokens context window at inference). As opposed to long-context-inference, training on very long context input prompts is quickly limited by GPU memory availability and by the prohibitively long training times it requires on state-of-the-art hardware. Meanwhile, many real-life applications require not only inference but also training/fine-tuning with long context on specific tasks. Such applications include, for example, augmenting the context with various sources of raw reference information for fact extraction, fact summarization, or fact reconciliation tasks. We propose adjoint sharding, a novel technique that comprises sharding gradient calculation during training to reduce memory requirements by orders of magnitude, making training on very long context computationally tractable. Adjoint sharding is based on the adjoint method and computes equivalent gradients to backpropagation. We also propose truncated adjoint sharding to speed up the algorithm while maintaining performance. We provide a distributed version, and a paralleled version of adjoint sharding to further speed up training. Empirical results show the proposed adjoint sharding algorithm reduces memory usage by up to 3X with a 1.27B parameter large language model on 1M context length training. This allows to increase the maximum context length during training or fine-tuning of a 1.27B parameter model from 35K tokens to above 100K tokens on a training infrastructure composed of five AWS P4 instances.

Learning the Target Network in Function Space

We focus on the task of learning the value function in the reinforcement learning (RL) setting. This task is often solved by updating a pair of online and target networks while ensuring that the parameters of these two networks are equivalent. We propose Lookahead-Replicate (LR), a new value-function approximation algorithm that is agnostic to this parameter-space equivalence. Instead, the LR algorithm is designed to maintain an equivalence between the two networks in the function space. This value-based equivalence is obtained by employing a new target-network update. We show that LR leads to a convergent behavior in learning the value function. We also present empirical results demonstrating that LR-based target-network updates significantly improve deep RL on the Atari benchmark.

TAIL: Task-specific Adapters for Imitation Learning with Large Pretrained Models

The full potential of large pretrained models remains largely untapped in control domains like robotics. This is mainly because of the scarcity of data and the computational challenges associated with training or fine-tuning these large models for such applications. Prior work mainly emphasizes effective pretraining of large models for decision-making, with little exploration into how to perform data-efficient continual adaptation of these models for new tasks. Recognizing these constraints, we introduce TAIL (Task-specific Adapters for Imitation Learning), a framework for efficient adaptation to new control tasks. Inspired by recent advancements in parameter-efficient fine-tuning in language domains, we explore efficient fine-tuning techniques -- e.g., Bottleneck Adapters, P-Tuning, and Low-Rank Adaptation (LoRA) -- in TAIL to adapt large pretrained models for new tasks with limited demonstration data. Our extensive experiments in large-scale language-conditioned manipulation tasks comparing prevalent parameter-efficient fine-tuning techniques and adaptation baselines suggest that TAIL with LoRA can achieve the best post-adaptation performance with only 1\% of the trainable parameters of full fine-tuning, while avoiding catastrophic forgetting and preserving adaptation plasticity in continual learning settings.

Resetting the Optimizer in Deep RL: An Empirical Study

We focus on the task of approximating the optimal value function in deep reinforcement learning. This iterative process is comprised of approximately solving a sequence of optimization problems where the objective function can change per iteration. The common approach to solving the problem is to employ modern variants of the stochastic gradient descent algorithm such as Adam. These optimizers maintain their own internal parameters such as estimates of the first and the second moment of the gradient, and update these parameters over time. Therefore, information obtained in previous iterations is being used to solve the optimization problem in the current iteration. We hypothesize that this can contaminate the internal parameters of the employed optimizer in situations where the optimization landscape of the previous iterations is quite different from the current iteration. To hedge against this effect, a simple idea is to reset the internal parameters of the optimizer when starting a new iteration. We empirically investigate this resetting strategy by employing various optimizers in conjunction with the Rainbow algorithm. We demonstrate that this simple modification unleashes the true potential of modern optimizers, and significantly improves the performance of deep RL on the Atari benchmark.

TD Convergence: An Optimization Perspective

We study the convergence behavior of the celebrated temporal-difference (TD) learning algorithm. By looking at the algorithm through the lens of optimization, we first argue that TD can be viewed as an iterative optimization algorithm where the function to be minimized changes per iteration. By carefully investigating the divergence displayed by TD on a classical counter example, we identify two forces that determine the convergent or divergent behavior of the algorithm. We next formalize our discovery in the linear TD setting with quadratic loss and prove that convergence of TD hinges on the interplay between these two forces. We extend this optimization perspective to prove convergence of TD in a much broader setting than just linear approximation and squared loss. Our results provide a theoretical explanation for the successful application of TD in reinforcement learning.

Characterizing the Action-Generalization Gap in Deep Q-Learning

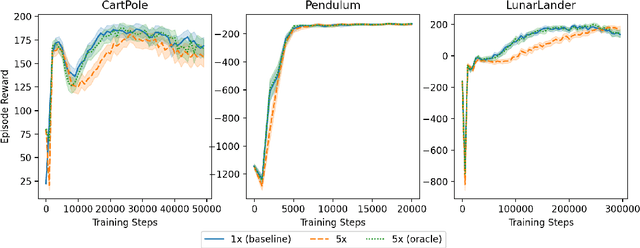
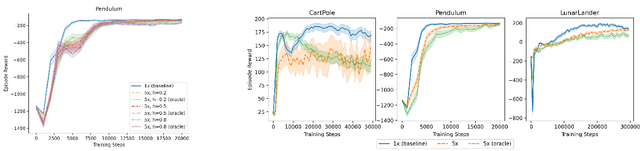
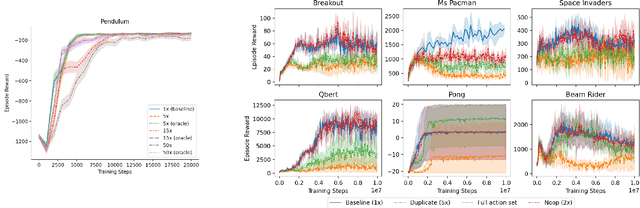
We study the action generalization ability of deep Q-learning in discrete action spaces. Generalization is crucial for efficient reinforcement learning (RL) because it allows agents to use knowledge learned from past experiences on new tasks. But while function approximation provides deep RL agents with a natural way to generalize over state inputs, the same generalization mechanism does not apply to discrete action outputs. And yet, surprisingly, our experiments indicate that Deep Q-Networks (DQN), which use exactly this type of function approximator, are still able to achieve modest action generalization. Our main contribution is twofold: first, we propose a method of evaluating action generalization using expert knowledge of action similarity, and empirically confirm that action generalization leads to faster learning; second, we characterize the action-generalization gap (the difference in learning performance between DQN and the expert) in different domains. We find that DQN can indeed generalize over actions in several simple domains, but that its ability to do so decreases as the action space grows larger.