Coarse-Grained Smoothness for RL in Metric Spaces
Paper and Code
Oct 23, 2021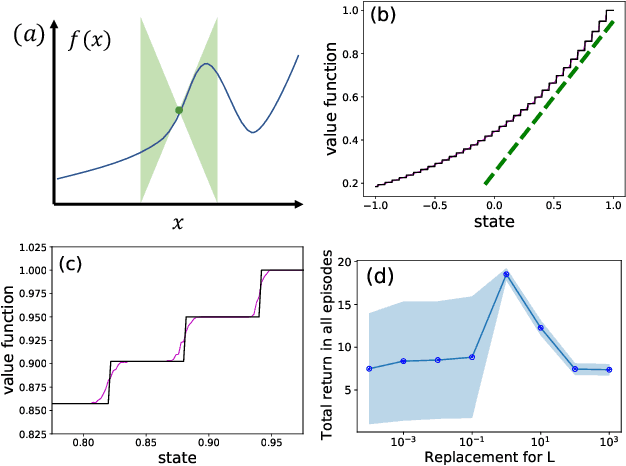
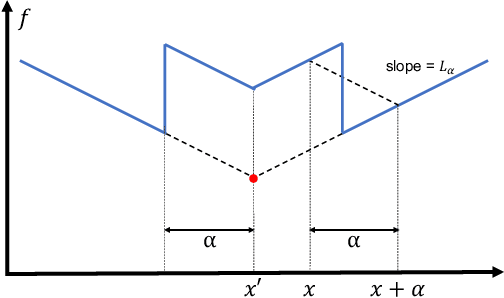
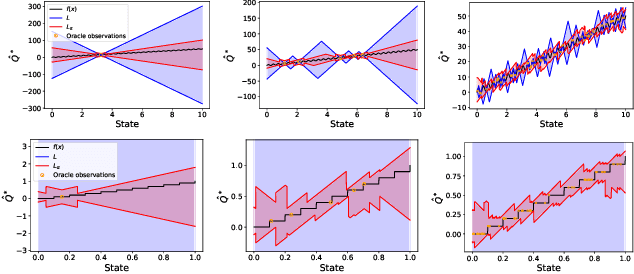
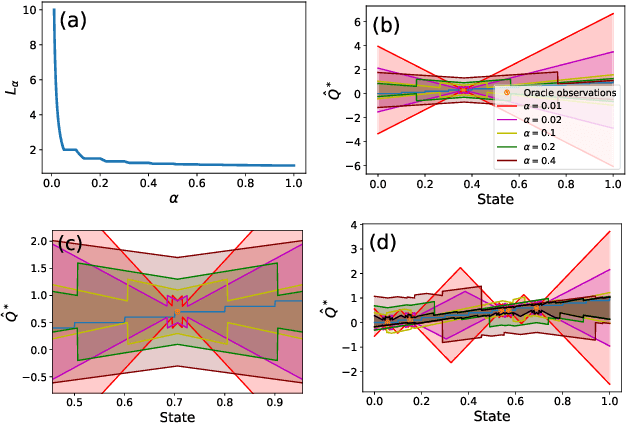
Principled decision-making in continuous state--action spaces is impossible without some assumptions. A common approach is to assume Lipschitz continuity of the Q-function. We show that, unfortunately, this property fails to hold in many typical domains. We propose a new coarse-grained smoothness definition that generalizes the notion of Lipschitz continuity, is more widely applicable, and allows us to compute significantly tighter bounds on Q-functions, leading to improved learning. We provide a theoretical analysis of our new smoothness definition, and discuss its implications and impact on control and exploration in continuous domains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge