Marina Meila
Local EGOP for Continuous Index Learning
Jan 11, 2026Abstract:We introduce the setting of continuous index learning, in which a function of many variables varies only along a small number of directions at each point. For efficient estimation, it is beneficial for a learning algorithm to adapt, near each point $x$, to the subspace that captures the local variability of the function $f$. We pose this task as kernel adaptation along a manifold with noise, and introduce Local EGOP learning, a recursive algorithm that utilizes the Expected Gradient Outer Product (EGOP) quadratic form as both a metric and inverse-covariance of our target distribution. We prove that Local EGOP learning adapts to the regularity of the function of interest, showing that under a supervised noisy manifold hypothesis, intrinsic dimensional learning rates are achieved for arbitrarily high-dimensional noise. Empirically, we compare our algorithm to the feature learning capabilities of deep learning. Additionally, we demonstrate improved regression quality compared to two-layer neural networks in the continuous single-index setting.
Cryo-em images are intrinsically low dimensional
Apr 15, 2025Abstract:Simulation-based inference provides a powerful framework for cryo-electron microscopy, employing neural networks in methods like CryoSBI to infer biomolecular conformations via learned latent representations. This latent space represents a rich opportunity, encoding valuable information about the physical system and the inference process. Harnessing this potential hinges on understanding the underlying geometric structure of these representations. We investigate this structure by applying manifold learning techniques to CryoSBI representations of hemagglutinin (simulated and experimental). We reveal that these high-dimensional data inherently populate low-dimensional, smooth manifolds, with simulated data effectively covering the experimental counterpart. By characterizing the manifold's geometry using Diffusion Maps and identifying its principal axes of variation via coordinate interpretation methods, we establish a direct link between the latent structure and key physical parameters. Discovering this intrinsic low-dimensionality and interpretable geometric organization not only validates the CryoSBI approach but enables us to learn more from the data structure and provides opportunities for improving future inference strategies by exploiting this revealed manifold geometry.
Isometry pursuit
Nov 27, 2024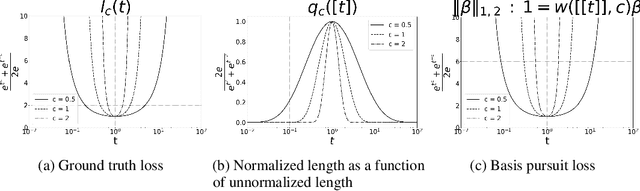
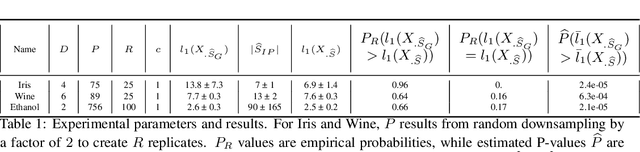
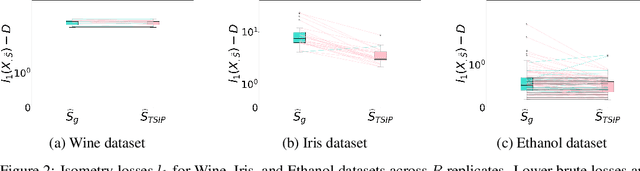

Abstract:Isometry pursuit is a convex algorithm for identifying orthonormal column-submatrices of wide matrices. It consists of a novel normalization method followed by multitask basis pursuit. Applied to Jacobians of putative coordinate functions, it helps identity isometric embeddings from within interpretable dictionaries. We provide theoretical and experimental results justifying this method. For problems involving coordinate selection and diversification, it offers a synergistic alternative to greedy and brute force search.
Dictionary-based Manifold Learning
Feb 04, 2023
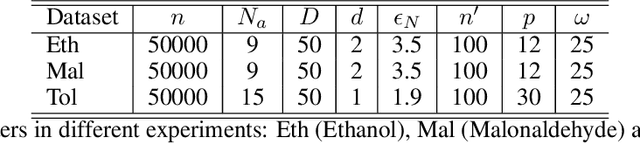

Abstract:We propose a paradigm for interpretable Manifold Learning for scientific data analysis, whereby we parametrize a manifold with $d$ smooth functions from a scientist-provided dictionary of meaningful, domain-related functions. When such a parametrization exists, we provide an algorithm for finding it based on sparse non-linear regression in the manifold tangent bundle, bypassing more standard manifold learning algorithms. We also discuss conditions for the existence of such parameterizations in function space and for successful recovery from finite samples. We demonstrate our method with experimental results from a real scientific domain.
The Parametric Stability of Well-separated Spherical Gaussian Mixtures
Feb 01, 2023


Abstract:We quantify the parameter stability of a spherical Gaussian Mixture Model (sGMM) under small perturbations in distribution space. Namely, we derive the first explicit bound to show that for a mixture of spherical Gaussian $P$ (sGMM) in a pre-defined model class, all other sGMM close to $P$ in this model class in total variation distance has a small parameter distance to $P$. Further, this upper bound only depends on $P$. The motivation for this work lies in providing guarantees for fitting Gaussian mixtures; with this aim in mind, all the constants involved are well defined and distribution free conditions for fitting mixtures of spherical Gaussians. Our results tighten considerably the existing computable bounds, and asymptotically match the known sharp thresholds for this problem.
Double Diffusion Maps and their Latent Harmonics for Scientific Computations in Latent Space
Apr 26, 2022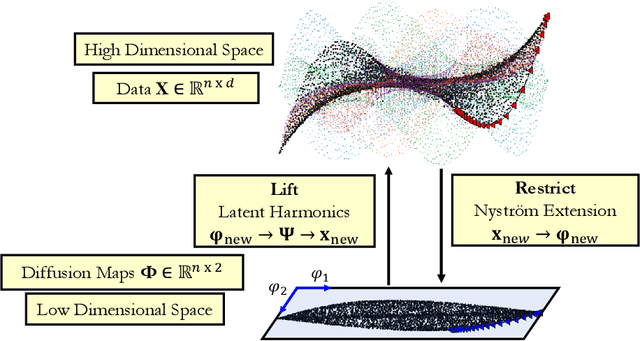

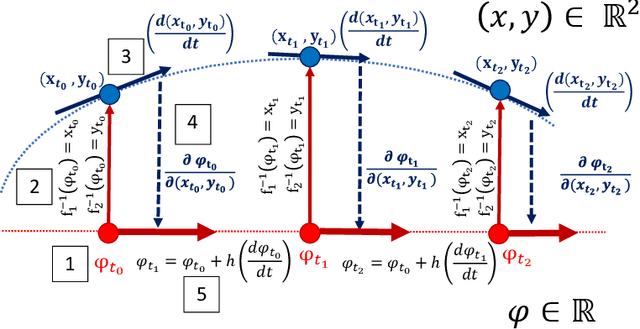

Abstract:We introduce a data-driven approach to building reduced dynamical models through manifold learning; the reduced latent space is discovered using Diffusion Maps (a manifold learning technique) on time series data. A second round of Diffusion Maps on those latent coordinates allows the approximation of the reduced dynamical models. This second round enables mapping the latent space coordinates back to the full ambient space (what is called lifting); it also enables the approximation of full state functions of interest in terms of the reduced coordinates. In our work, we develop and test three different reduced numerical simulation methodologies, either through pre-tabulation in the latent space and integration on the fly or by going back and forth between the ambient space and the latent space. The data-driven latent space simulation results, based on the three different approaches, are validated through (a) the latent space observation of the full simulation through the Nystr\"om Extension formula, or through (b) lifting the reduced trajectory back to the full ambient space, via Latent Harmonics. Latent space modeling often involves additional regularization to favor certain properties of the space over others, and the mapping back to the ambient space is then constructed mostly independently from these properties; here, we use the same data-driven approach to construct the latent space and then map back to the ambient space.
A class of network models recoverable by spectral clustering
Apr 21, 2021Abstract:Finding communities in networks is a problem that remains difficult, in spite of the amount of attention it has recently received. The Stochastic Block-Model (SBM) is a generative model for graphs with "communities" for which, because of its simplicity, the theoretical understanding has advanced fast in recent years. In particular, there have been various results showing that simple versions of spectral clustering using the Normalized Laplacian of the graph can recover the communities almost perfectly with high probability. Here we show that essentially the same algorithm used for the SBM and for its extension called Degree-Corrected SBM, works on a wider class of Block-Models, which we call Preference Frame Models, with essentially the same guarantees. Moreover, the parametrization we introduce clearly exhibits the free parameters needed to specify this class of models, and results in bounds that expose with more clarity the parameters that control the recovery error in this model class.
Guarantees for Hierarchical Clustering by the Sublevel Set method
Jul 06, 2020Abstract:Meila (2018) introduces an optimization based method called the Sublevel Set method, to guarantee that a clustering is nearly optimal and "approximately correct" without relying on any assumptions about the distribution that generated the data. This paper extends the Sublevel Set method to the cost-based hierarchical clustering paradigm proposed by Dasgupta (2016).
A regression approach for explaining manifold embedding coordinates
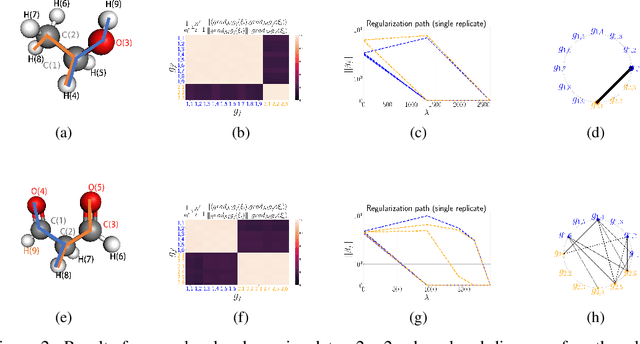
Nov 29, 2018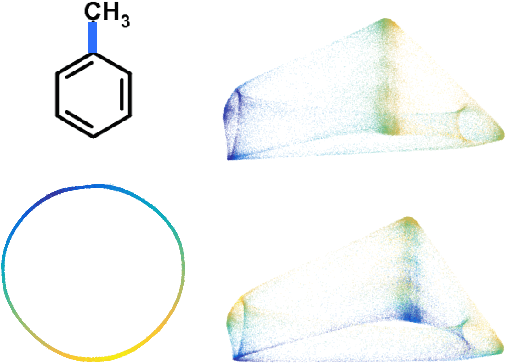
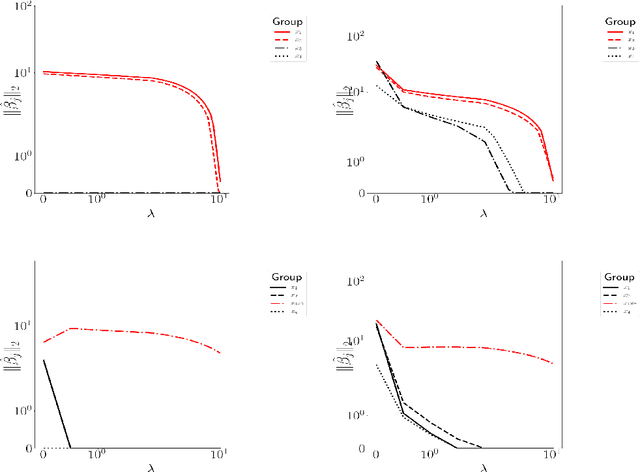

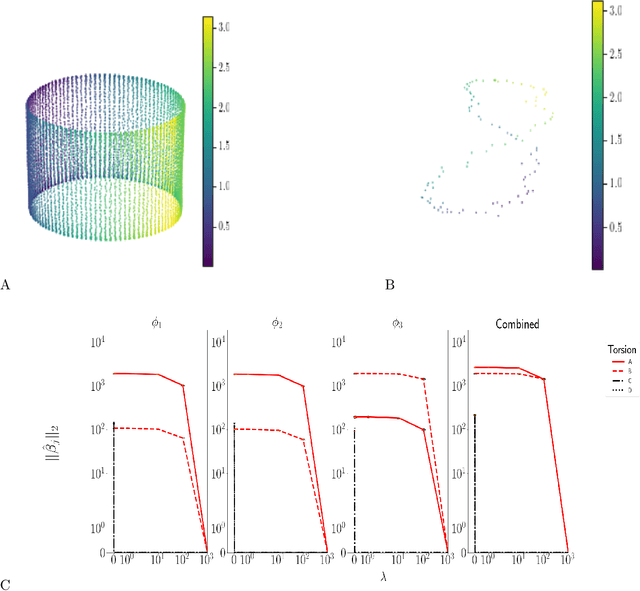
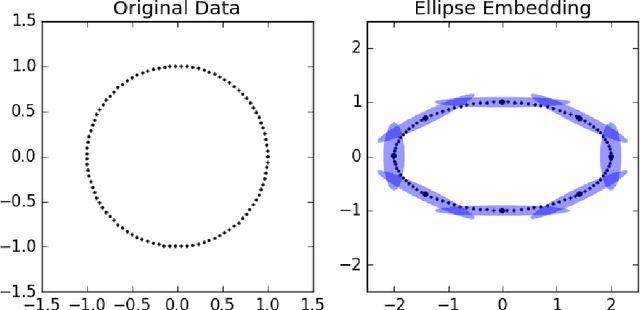
Abstract:Manifold embedding algorithms map high dimensional data, down to coordinates in a much lower dimensional space. One of the aims of the dimension reduction is to find the {\em intrinsic coordinates} that describe the data manifold. However, the coordinates returned by the embedding algorithm are abstract coordinates. Finding their physical, domain related meaning is not formalized and left to the domain experts. This paper studies the problem of recovering the domain-specific meaning of the new low dimensional representation in a semi-automatic, principled fashion. We propose a method to explain embedding coordinates on a manifold as {\em non-linear} compositions of functions from a user-defined dictionary. We show that this problem can be set up as a sparse {\em linear Group Lasso} recovery problem, find sufficient recovery conditions, and demonstrate its effectiveness on data.
megaman: Manifold Learning with Millions of points
Mar 09, 2016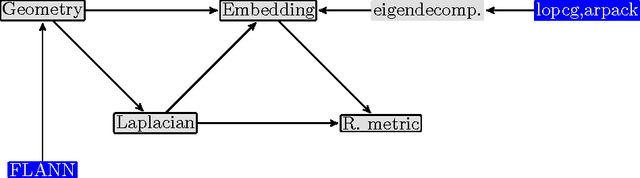
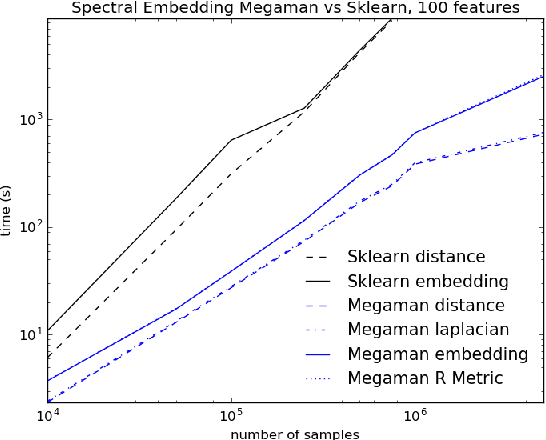
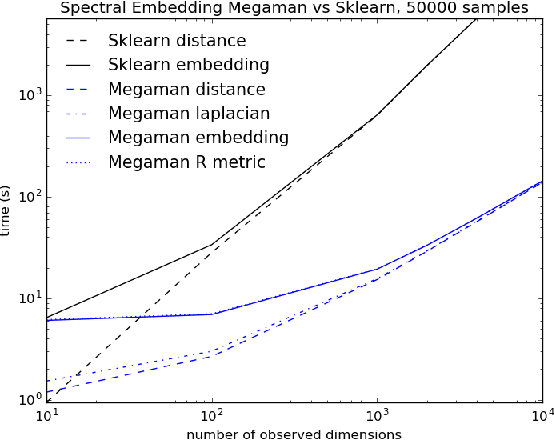
Abstract:Manifold Learning is a class of algorithms seeking a low-dimensional non-linear representation of high-dimensional data. Thus manifold learning algorithms are, at least in theory, most applicable to high-dimensional data and sample sizes to enable accurate estimation of the manifold. Despite this, most existing manifold learning implementations are not particularly scalable. Here we present a Python package that implements a variety of manifold learning algorithms in a modular and scalable fashion, using fast approximate neighbors searches and fast sparse eigendecompositions. The package incorporates theoretical advances in manifold learning, such as the unbiased Laplacian estimator and the estimation of the embedding distortion by the Riemannian metric method. In benchmarks, even on a single-core desktop computer, our code embeds millions of data points in minutes, and takes just 200 minutes to embed the main sample of galaxy spectra from the Sloan Digital Sky Survey --- consisting of 0.6 million samples in 3750-dimensions --- a task which has not previously been possible.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge