A regression approach for explaining manifold embedding coordinates

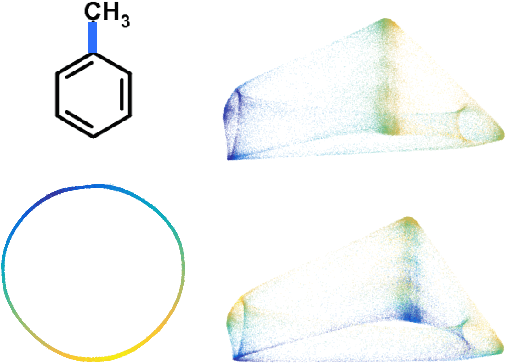
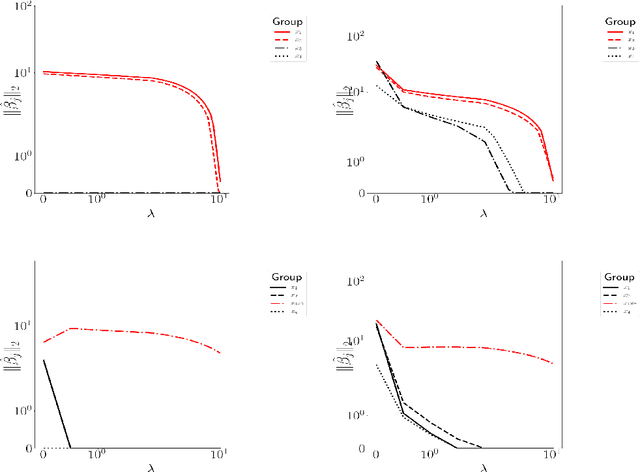
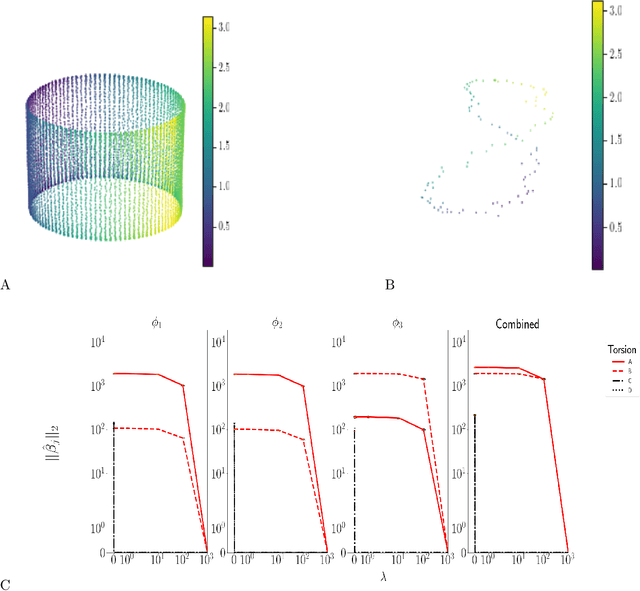
Manifold embedding algorithms map high dimensional data, down to coordinates in a much lower dimensional space. One of the aims of the dimension reduction is to find the {\em intrinsic coordinates} that describe the data manifold. However, the coordinates returned by the embedding algorithm are abstract coordinates. Finding their physical, domain related meaning is not formalized and left to the domain experts. This paper studies the problem of recovering the domain-specific meaning of the new low dimensional representation in a semi-automatic, principled fashion. We propose a method to explain embedding coordinates on a manifold as {\em non-linear} compositions of functions from a user-defined dictionary. We show that this problem can be set up as a sparse {\em linear Group Lasso} recovery problem, find sufficient recovery conditions, and demonstrate its effectiveness on data.