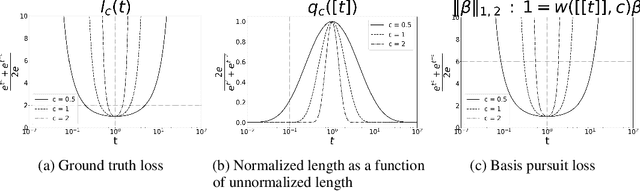
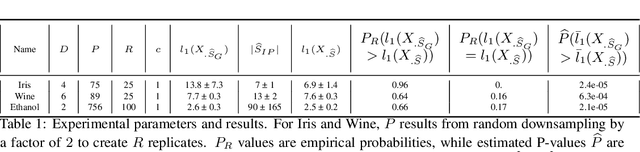
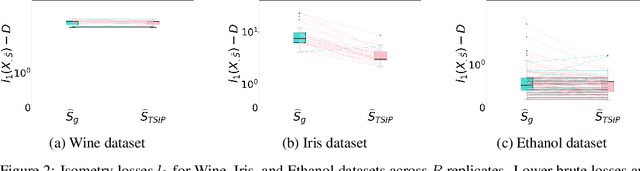
Isometry pursuit

Isometry pursuit is a convex algorithm for identifying orthonormal column-submatrices of wide matrices. It consists of a novel normalization method followed by multitask basis pursuit. Applied to Jacobians of putative coordinate functions, it helps identity isometric embeddings from within interpretable dictionaries. We provide theoretical and experimental results justifying this method. For problems involving coordinate selection and diversification, it offers a synergistic alternative to greedy and brute force search.

Dictionary-based Manifold Learning

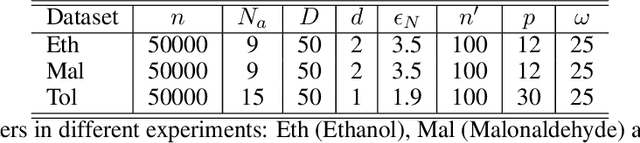
We propose a paradigm for interpretable Manifold Learning for scientific data analysis, whereby we parametrize a manifold with $d$ smooth functions from a scientist-provided dictionary of meaningful, domain-related functions. When such a parametrization exists, we provide an algorithm for finding it based on sparse non-linear regression in the manifold tangent bundle, bypassing more standard manifold learning algorithms. We also discuss conditions for the existence of such parameterizations in function space and for successful recovery from finite samples. We demonstrate our method with experimental results from a real scientific domain.

A regression approach for explaining manifold embedding coordinates

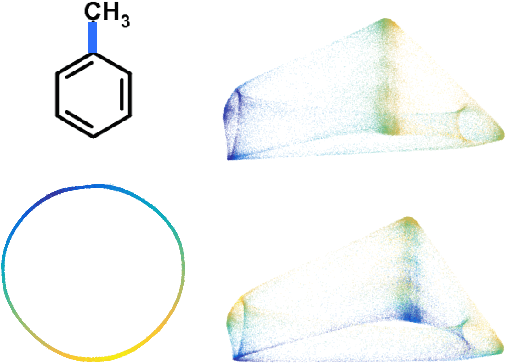
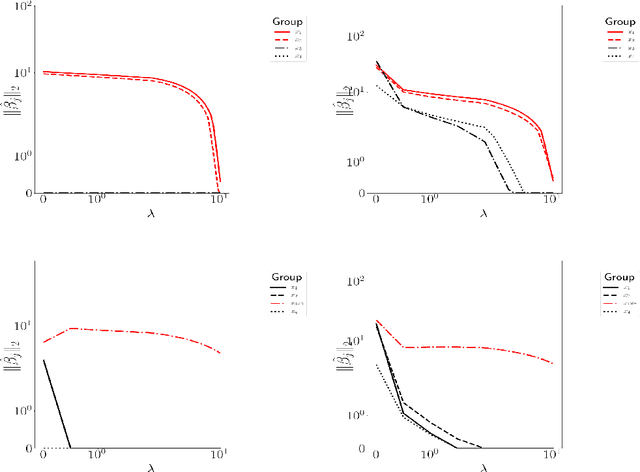
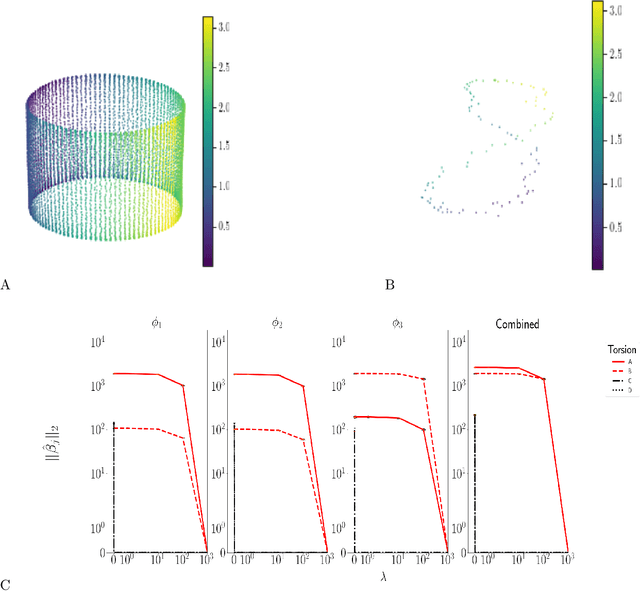
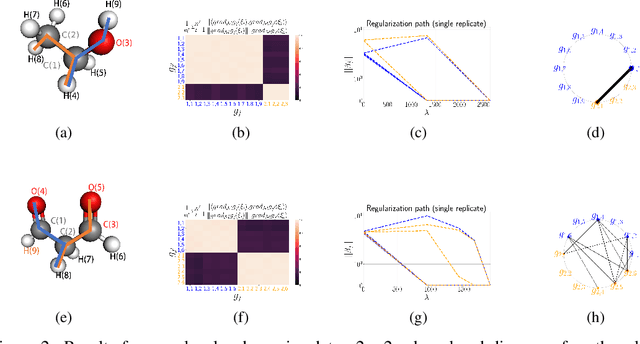
Manifold embedding algorithms map high dimensional data, down to coordinates in a much lower dimensional space. One of the aims of the dimension reduction is to find the {\em intrinsic coordinates} that describe the data manifold. However, the coordinates returned by the embedding algorithm are abstract coordinates. Finding their physical, domain related meaning is not formalized and left to the domain experts. This paper studies the problem of recovering the domain-specific meaning of the new low dimensional representation in a semi-automatic, principled fashion. We propose a method to explain embedding coordinates on a manifold as {\em non-linear} compositions of functions from a user-defined dictionary. We show that this problem can be set up as a sparse {\em linear Group Lasso} recovery problem, find sufficient recovery conditions, and demonstrate its effectiveness on data.