Isometry pursuit
Paper and Code
Nov 27, 2024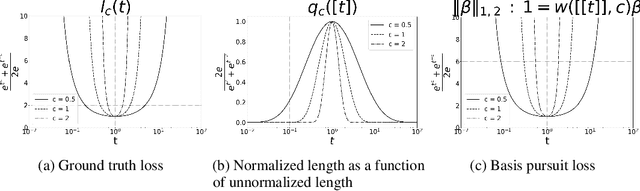
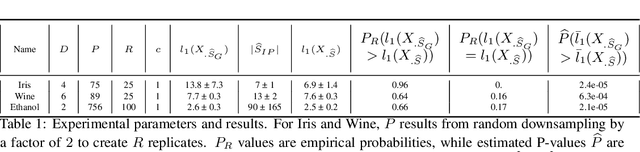
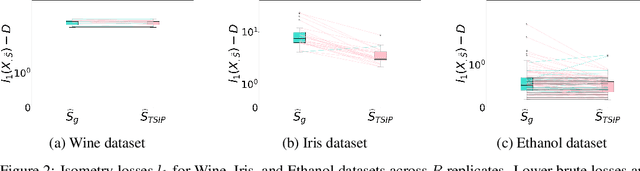

Isometry pursuit is a convex algorithm for identifying orthonormal column-submatrices of wide matrices. It consists of a novel normalization method followed by multitask basis pursuit. Applied to Jacobians of putative coordinate functions, it helps identity isometric embeddings from within interpretable dictionaries. We provide theoretical and experimental results justifying this method. For problems involving coordinate selection and diversification, it offers a synergistic alternative to greedy and brute force search.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge