Dictionary-based Manifold Learning
Paper and Code
Feb 04, 2023
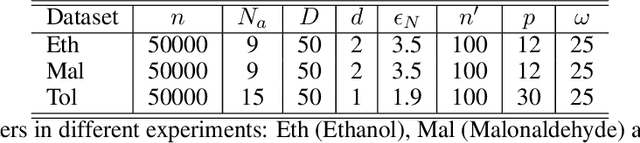
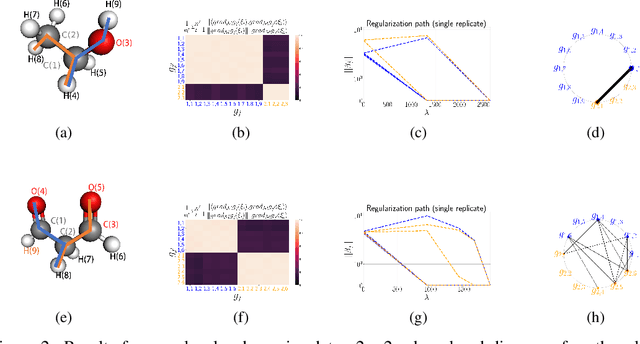

We propose a paradigm for interpretable Manifold Learning for scientific data analysis, whereby we parametrize a manifold with $d$ smooth functions from a scientist-provided dictionary of meaningful, domain-related functions. When such a parametrization exists, we provide an algorithm for finding it based on sparse non-linear regression in the manifold tangent bundle, bypassing more standard manifold learning algorithms. We also discuss conditions for the existence of such parameterizations in function space and for successful recovery from finite samples. We demonstrate our method with experimental results from a real scientific domain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge