Energy-GNoME: A Living Database of Selected Materials for Energy Applications

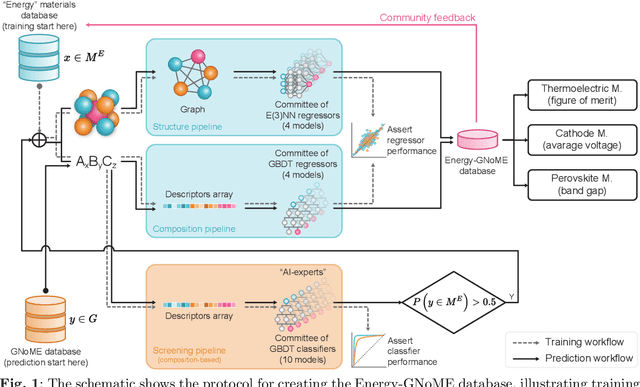
Artificial Intelligence (AI) in materials science is driving significant advancements in the discovery of advanced materials for energy applications. The recent GNoME protocol identifies over 380,000 novel stable crystals. From this, we identify over 33,000 materials with potential as energy materials forming the Energy-GNoME database. Leveraging Machine Learning (ML) and Deep Learning (DL) tools, our protocol mitigates cross-domain data bias using feature spaces to identify potential candidates for thermoelectric materials, novel battery cathodes, and novel perovskites. Classifiers with both structural and compositional features identify domains of applicability, where we expect enhanced accuracy of the regressors. Such regressors are trained to predict key materials properties like, thermoelectric figure of merit (zT), band gap (Eg), and cathode voltage ($\Delta V_c$). This method significantly narrows the pool of potential candidates, serving as an efficient guide for experimental and computational chemistry investigations and accelerating the discovery of materials suited for electricity generation, energy storage and conversion.

Learning effective good variables from physical data

We assume that a sufficiently large database is available, where a physical property of interest and a number of associated ruling primitive variables or observables are stored. We introduce and test two machine learning approaches to discover possible groups or combinations of primitive variables: The first approach is based on regression models whereas the second on classification models. The variable group (here referred to as the new effective good variable) can be considered as successfully found, when the physical property of interest is characterized by the following effective invariant behaviour: In the first method, invariance of the group implies invariance of the property up to a given accuracy; in the other method, upon partition of the physical property values into two or more classes, invariance of the group implies invariance of the class. For the sake of illustration, the two methods are successfully applied to two popular empirical correlations describing the convective heat transfer phenomenon and to the Newton's law of universal gravitation.

On some elusive aspects of databases hindering AI based discovery: A case study on superconducting materials

It stands to reason that the amount and the quality of big data is of key importance for setting up accurate AI-driven models. Nonetheless, we believe there are still critical roadblocks in the inherent generation of databases, that are often underestimated and poorly discussed in the literature. In our view, such issues can seriously hinder the AI-based discovery process, even when high quality, sufficiently large and highly reputable data sources are available. Here, considering superconducting and thermoelectric materials as two representative case studies, we specifically discuss three aspects, namely intrinsically biased sample selection, possible hidden variables, disparate data age. Importantly, to our knowledge, we suggest and test a first strategy capable of detecting and quantifying the presence of the intrinsic data bias.

Double Diffusion Maps and their Latent Harmonics for Scientific Computations in Latent Space

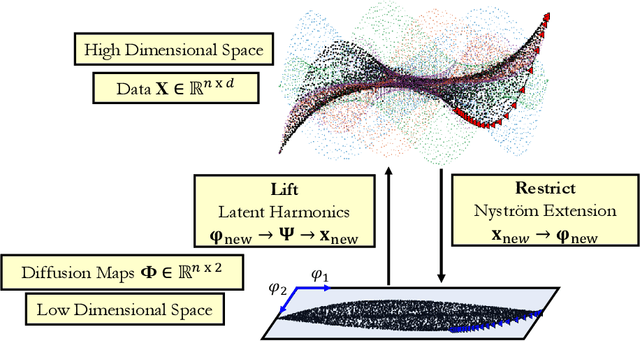
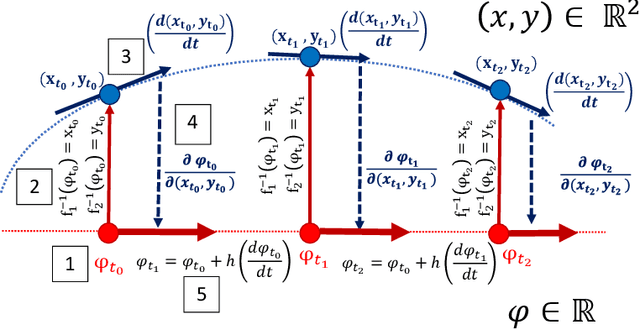
We introduce a data-driven approach to building reduced dynamical models through manifold learning; the reduced latent space is discovered using Diffusion Maps (a manifold learning technique) on time series data. A second round of Diffusion Maps on those latent coordinates allows the approximation of the reduced dynamical models. This second round enables mapping the latent space coordinates back to the full ambient space (what is called lifting); it also enables the approximation of full state functions of interest in terms of the reduced coordinates. In our work, we develop and test three different reduced numerical simulation methodologies, either through pre-tabulation in the latent space and integration on the fly or by going back and forth between the ambient space and the latent space. The data-driven latent space simulation results, based on the three different approaches, are validated through (a) the latent space observation of the full simulation through the Nystr\"om Extension formula, or through (b) lifting the reduced trajectory back to the full ambient space, via Latent Harmonics. Latent space modeling often involves additional regularization to favor certain properties of the space over others, and the mapping back to the ambient space is then constructed mostly independently from these properties; here, we use the same data-driven approach to construct the latent space and then map back to the ambient space.