Energy-GNoME: A Living Database of Selected Materials for Energy Applications

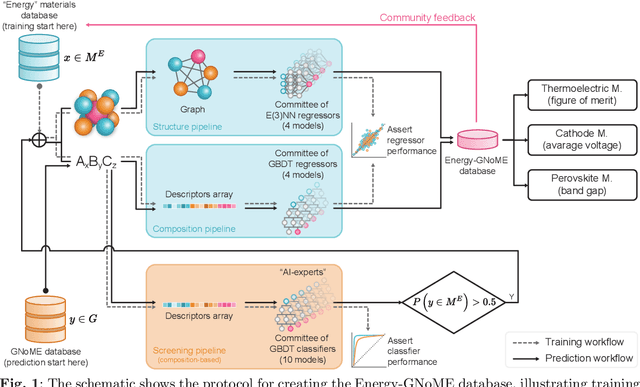
Artificial Intelligence (AI) in materials science is driving significant advancements in the discovery of advanced materials for energy applications. The recent GNoME protocol identifies over 380,000 novel stable crystals. From this, we identify over 33,000 materials with potential as energy materials forming the Energy-GNoME database. Leveraging Machine Learning (ML) and Deep Learning (DL) tools, our protocol mitigates cross-domain data bias using feature spaces to identify potential candidates for thermoelectric materials, novel battery cathodes, and novel perovskites. Classifiers with both structural and compositional features identify domains of applicability, where we expect enhanced accuracy of the regressors. Such regressors are trained to predict key materials properties like, thermoelectric figure of merit (zT), band gap (Eg), and cathode voltage ($\Delta V_c$). This method significantly narrows the pool of potential candidates, serving as an efficient guide for experimental and computational chemistry investigations and accelerating the discovery of materials suited for electricity generation, energy storage and conversion.

Learning effective good variables from physical data

We assume that a sufficiently large database is available, where a physical property of interest and a number of associated ruling primitive variables or observables are stored. We introduce and test two machine learning approaches to discover possible groups or combinations of primitive variables: The first approach is based on regression models whereas the second on classification models. The variable group (here referred to as the new effective good variable) can be considered as successfully found, when the physical property of interest is characterized by the following effective invariant behaviour: In the first method, invariance of the group implies invariance of the property up to a given accuracy; in the other method, upon partition of the physical property values into two or more classes, invariance of the group implies invariance of the class. For the sake of illustration, the two methods are successfully applied to two popular empirical correlations describing the convective heat transfer phenomenon and to the Newton's law of universal gravitation.