Safety-Critical Learning for Long-Tail Events: The TUM Traffic Accident Dataset

Even though a significant amount of work has been done to increase the safety of transportation networks, accidents still occur regularly. They must be understood as an unavoidable and sporadic outcome of traffic networks. We present the TUM Traffic Accident (TUMTraf-A) dataset, a collection of real-world highway accidents. It contains ten sequences of vehicle crashes at high-speed driving with 294,924 labeled 2D and 93,012 labeled 3D boxes and track IDs within 48,144 labeled frames recorded from four roadside cameras and LiDARs at 10 Hz. The dataset contains ten object classes and is provided in the OpenLABEL format. We propose Accid3nD, an accident detection model that combines a rule-based approach with a learning-based one. Experiments and ablation studies on our dataset show the robustness of our proposed method. The dataset, model, and code are available on our project website: https://tum-traffic-dataset.github.io/tumtraf-a.

Towards Vision Zero: The Accid3nD Dataset

Even though a significant amount of work has been done to increase the safety of transportation networks, accidents still occur regularly. They must be understood as unavoidable and sporadic outcomes of traffic networks. No public dataset contains 3D annotations of real-world accidents recorded from roadside sensors. We present the Accid3nD dataset, a collection of real-world highway accidents in different weather and lighting conditions. It contains vehicle crashes at high-speed driving with 2,634,233 labeled 2D bounding boxes, instance masks, and 3D bounding boxes with track IDs. In total, the dataset contains 111,945 labeled frames recorded from four roadside cameras and LiDARs at 25 Hz. The dataset contains six object classes and is provided in the OpenLABEL format. We propose an accident detection model that combines a rule-based approach with a learning-based one. Experiments and ablation studies on our dataset show the robustness of our proposed method. The dataset, model, and code are available on our website: https://accident-dataset.github.io.

Data-driven modelling of brain activity using neural networks, Diffusion Maps, and the Koopman operator

We propose a machine-learning approach to model long-term out-of-sample dynamics of brain activity from task-dependent fMRI data. Our approach is a three stage one. First, we exploit Diffusion maps (DMs) to discover a set of variables that parametrize the low-dimensional manifold on which the emergent high-dimensional fMRI time series evolve. Then, we construct reduced-order-models (ROMs) on the embedded manifold via two techniques: Feedforward Neural Networks (FNNs) and the Koopman operator. Finally, for predicting the out-of-sample long-term dynamics of brain activity in the ambient fMRI space, we solve the pre-image problem coupling DMs with Geometric Harmonics (GH) when using FNNs and the Koopman modes per se. For our illustrations, we have assessed the performance of the two proposed schemes using a benchmark fMRI dataset with recordings during a visuo-motor task. The results suggest that just a few (for the particular task, five) non-linear coordinates of the high-dimensional fMRI time series provide a good basis for modelling and out-of-sample prediction of the brain activity. Furthermore, we show that the proposed approaches outperform the one-step ahead predictions of the naive random walk model, which, in contrast to our scheme, relies on the knowledge of the signals in the previous time step. Importantly, we show that the proposed Koopman operator approach provides, for any practical purposes, equivalent results to the FNN-GH approach, thus bypassing the need to train a non-linear map and to use GH to extrapolate predictions in the ambient fMRI space; one can use instead the low-frequency truncation of the DMs function space of L^2-integrable functions, to predict the entire list of coordinate functions in the fMRI space and to solve the pre-image problem.

Double Diffusion Maps and their Latent Harmonics for Scientific Computations in Latent Space

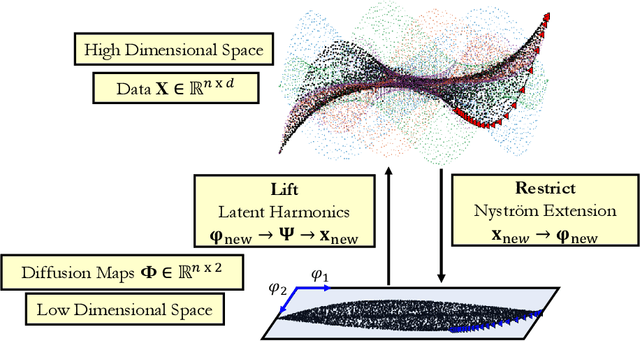
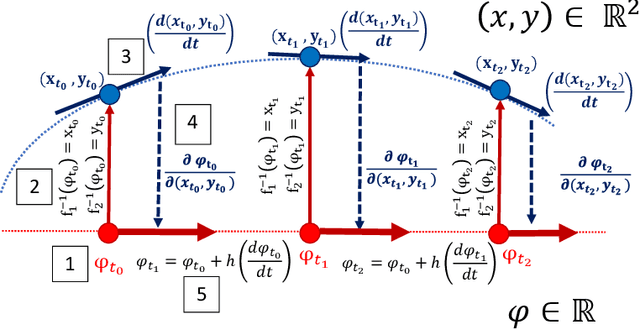
We introduce a data-driven approach to building reduced dynamical models through manifold learning; the reduced latent space is discovered using Diffusion Maps (a manifold learning technique) on time series data. A second round of Diffusion Maps on those latent coordinates allows the approximation of the reduced dynamical models. This second round enables mapping the latent space coordinates back to the full ambient space (what is called lifting); it also enables the approximation of full state functions of interest in terms of the reduced coordinates. In our work, we develop and test three different reduced numerical simulation methodologies, either through pre-tabulation in the latent space and integration on the fly or by going back and forth between the ambient space and the latent space. The data-driven latent space simulation results, based on the three different approaches, are validated through (a) the latent space observation of the full simulation through the Nystr\"om Extension formula, or through (b) lifting the reduced trajectory back to the full ambient space, via Latent Harmonics. Latent space modeling often involves additional regularization to favor certain properties of the space over others, and the mapping back to the ambient space is then constructed mostly independently from these properties; here, we use the same data-driven approach to construct the latent space and then map back to the ambient space.

Can we learn where people go?

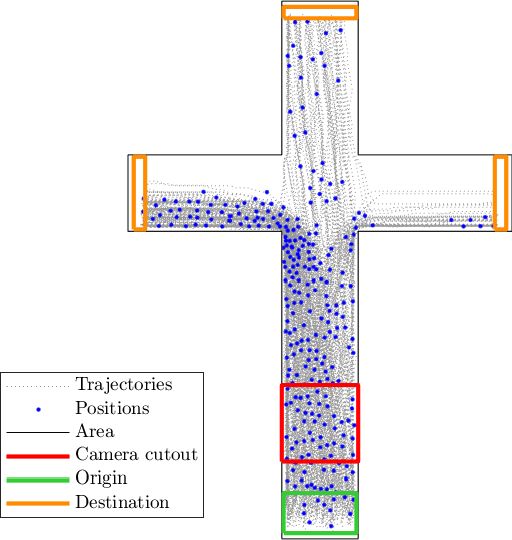
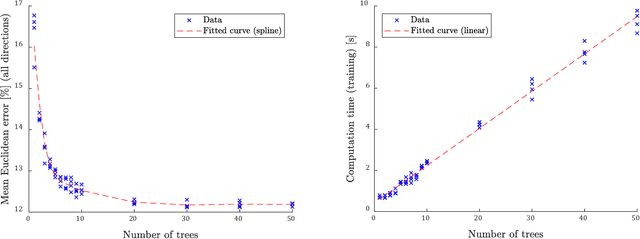
In most agent-based simulators, pedestrians navigate from origins to destinations. Consequently, destinations are essential input parameters to the simulation. While many other relevant parameters as positions, speeds and densities can be obtained from sensors, like cameras, destinations cannot be observed directly. Our research question is: Can we obtain this information from video data using machine learning methods? We use density heatmaps, which indicate the pedestrian density within a given camera cutout, as input to predict the destination distributions. For our proof of concept, we train a Random Forest predictor on an exemplary data set generated with the Vadere microscopic simulator. The scenario is a crossroad where pedestrians can head left, straight or right. In addition, we gain first insights on suitable placement of the camera. The results motivate an in-depth analysis of the methodology.