Cryo-em images are intrinsically low dimensional

Simulation-based inference provides a powerful framework for cryo-electron microscopy, employing neural networks in methods like CryoSBI to infer biomolecular conformations via learned latent representations. This latent space represents a rich opportunity, encoding valuable information about the physical system and the inference process. Harnessing this potential hinges on understanding the underlying geometric structure of these representations. We investigate this structure by applying manifold learning techniques to CryoSBI representations of hemagglutinin (simulated and experimental). We reveal that these high-dimensional data inherently populate low-dimensional, smooth manifolds, with simulated data effectively covering the experimental counterpart. By characterizing the manifold's geometry using Diffusion Maps and identifying its principal axes of variation via coordinate interpretation methods, we establish a direct link between the latent structure and key physical parameters. Discovering this intrinsic low-dimensionality and interpretable geometric organization not only validates the CryoSBI approach but enables us to learn more from the data structure and provides opportunities for improving future inference strategies by exploiting this revealed manifold geometry.

Sharp error estimates for target measure diffusion maps with applications to the committor problem

We obtain asymptotically sharp error estimates for the consistency error of the Target Measure Diffusion map (TMDmap) (Banisch et al. 2020), a variant of diffusion maps featuring importance sampling and hence allowing input data drawn from an arbitrary density. The derived error estimates include the bias error and the variance error. The resulting convergence rates are consistent with the approximation theory of graph Laplacians. The key novelty of our results lies in the explicit quantification of all the prefactors on leading-order terms. We also prove an error estimate for solutions of Dirichlet BVPs obtained using TMDmap, showing that the solution error is controlled by consistency error. We use these results to study an important application of TMDmap in the analysis of rare events in systems governed by overdamped Langevin dynamics using the framework of transition path theory (TPT). The cornerstone ingredient of TPT is the solution of the committor problem, a boundary value problem for the backward Kolmogorov PDE. Remarkably, we find that the TMDmap algorithm is particularly suited as a meshless solver to the committor problem due to the cancellation of several error terms in the prefactor formula. Furthermore, significant improvements in bias and variance errors occur when using a quasi-uniform sampling density. Our numerical experiments show that these improvements in accuracy are realizable in practice when using $\delta$-nets as spatially uniform inputs to the TMDmap algorithm.

Introducing dynamical constraints into representation learning

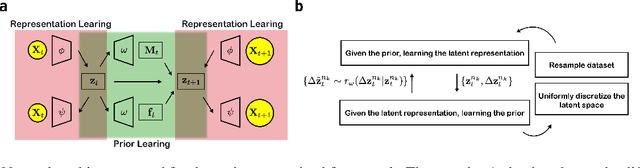
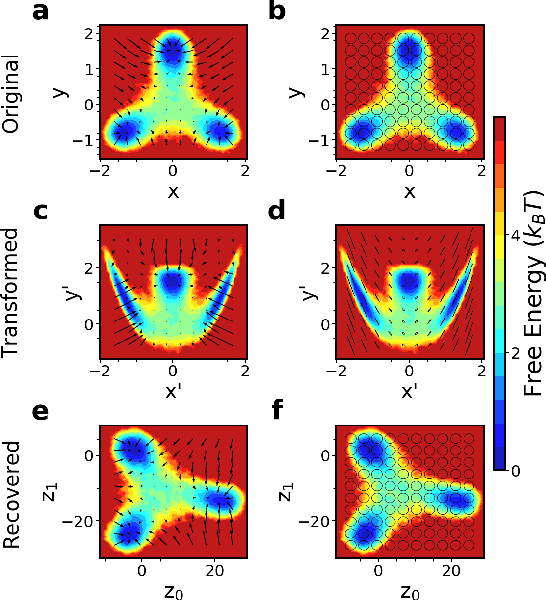
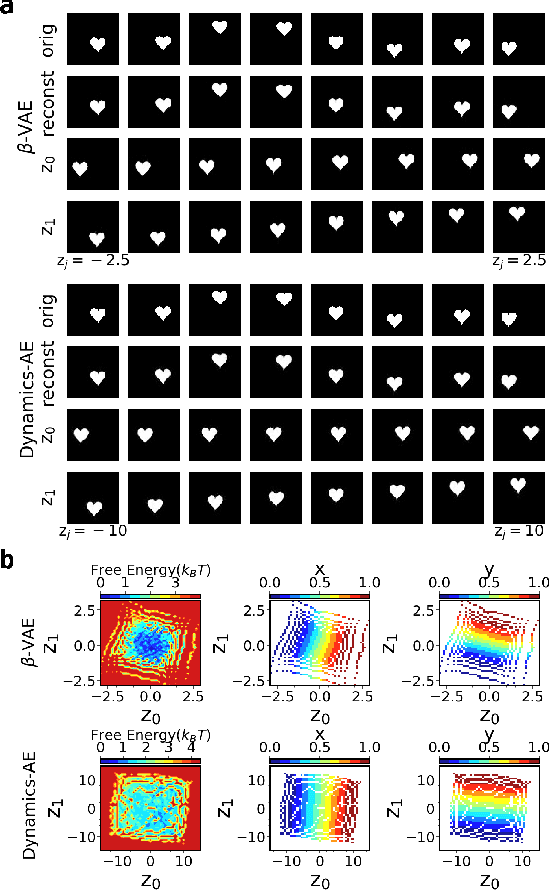
While representation learning has been central to the rise of machine learning and artificial intelligence, a key problem remains in making the learnt representations meaningful. For this the typical approach is to regularize the learned representation through prior probability distributions. However such priors are usually unavailable or ad hoc. To deal with this, we propose a dynamics-constrained representation learning framework. Instead of using predefined probabilities, we restrict the latent representation to follow specific dynamics, which is a more natural constraint for representation learning in dynamical systems. Our belief stems from a fundamental observation in physics that though different systems can have different marginalized probability distributions, they typically obey the same dynamics, such as Newton's and Schrodinger's equations. We validate our framework for different systems including a real-world fluorescent DNA movie dataset. We show that our algorithm can uniquely identify an uncorrelated, isometric and meaningful latent representation.