Neumann eigenmaps for landmark embedding

We present Neumann eigenmaps (NeuMaps), a novel approach for enhancing the standard diffusion map embedding using landmarks, i.e distinguished samples within the dataset. By interpreting these landmarks as a subgraph of the larger data graph, NeuMaps are obtained via the eigendecomposition of a renormalized Neumann Laplacian. We show that NeuMaps offer two key advantages: (1) they provide a computationally efficient embedding that accurately recovers the diffusion distance associated with the reflecting random walk on the subgraph, and (2) they naturally incorporate the Nystr\"om extension within the diffusion map framework through the discrete Neumann boundary condition. Through examples in digit classification and molecular dynamics, we demonstrate that NeuMaps not only improve upon existing landmark-based embedding methods but also enhance the stability of diffusion map embeddings to the removal of highly significant points.

Input layer regularization and automated regularization hyperparameter tuning for myelin water estimation using deep learning

We propose a novel deep learning method which combines classical regularization with data augmentation for estimating myelin water fraction (MWF) in the brain via biexponential analysis. Our aim is to design an accurate deep learning technique for analysis of signals arising in magnetic resonance relaxometry. In particular, we study the biexponential model, one of the signal models used for MWF estimation. We greatly extend our previous work on \emph{input layer regularization (ILR)} in several ways. We now incorporate optimal regularization parameter selection via a dedicated neural network or generalized cross validation (GCV) on a signal-by-signal, or pixel-by-pixel, basis to form the augmented input signal, and now incorporate estimation of MWF, rather than just exponential time constants, into the analysis. On synthetically generated data, our proposed deep learning architecture outperformed both classical methods and a conventional multi-layer perceptron. On in vivo brain data, our architecture again outperformed other comparison methods, with GCV proving to be somewhat superior to a NN for regularization parameter selection. Thus, ILR improves estimation of MWF within the biexponential model. In addition, classical methods such as GCV may be combined with deep learning to optimize MWF imaging in the human brain.

Sharp error estimates for target measure diffusion maps with applications to the committor problem

We obtain asymptotically sharp error estimates for the consistency error of the Target Measure Diffusion map (TMDmap) (Banisch et al. 2020), a variant of diffusion maps featuring importance sampling and hence allowing input data drawn from an arbitrary density. The derived error estimates include the bias error and the variance error. The resulting convergence rates are consistent with the approximation theory of graph Laplacians. The key novelty of our results lies in the explicit quantification of all the prefactors on leading-order terms. We also prove an error estimate for solutions of Dirichlet BVPs obtained using TMDmap, showing that the solution error is controlled by consistency error. We use these results to study an important application of TMDmap in the analysis of rare events in systems governed by overdamped Langevin dynamics using the framework of transition path theory (TPT). The cornerstone ingredient of TPT is the solution of the committor problem, a boundary value problem for the backward Kolmogorov PDE. Remarkably, we find that the TMDmap algorithm is particularly suited as a meshless solver to the committor problem due to the cancellation of several error terms in the prefactor formula. Furthermore, significant improvements in bias and variance errors occur when using a quasi-uniform sampling density. Our numerical experiments show that these improvements in accuracy are realizable in practice when using $\delta$-nets as spatially uniform inputs to the TMDmap algorithm.

Emergence of the SVD as an interpretable factorization in deep learning for inverse problems

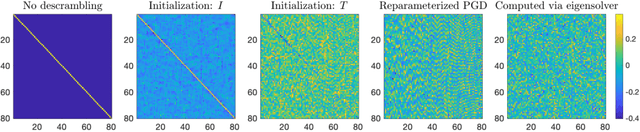
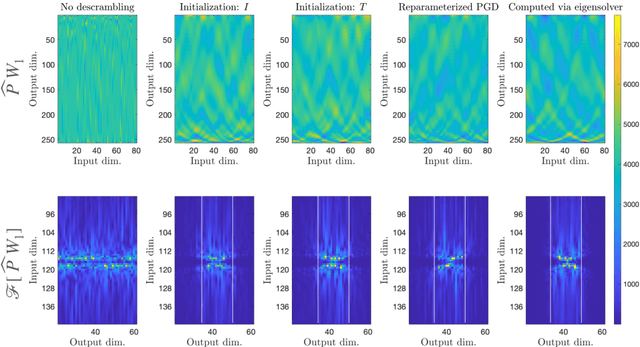
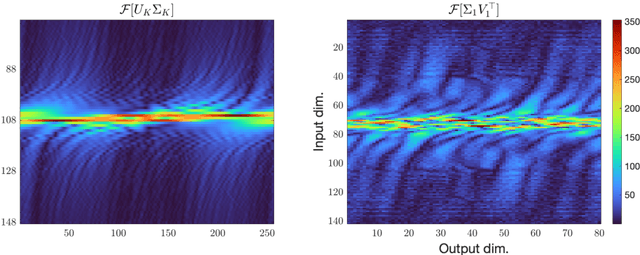
We demonstrate the emergence of weight matrix singular value decomposition (SVD) in interpreting neural networks (NNs) for parameter estimation from noisy signals. The SVD appears naturally as a consequence of initial application of a descrambling transform - a recently-developed technique for addressing interpretability in NNs \cite{amey2021neural}. We find that within the class of noisy parameter estimation problems, the SVD may be the means by which networks memorize the signal model. We substantiate our theoretical findings with empirical evidence from both linear and non-linear settings. Our results also illuminate the connections between a mathematical theory of semantic development \cite{saxe2019mathematical} and neural network interpretability.