Introducing dynamical constraints into representation learning
Paper and Code
Sep 02, 2022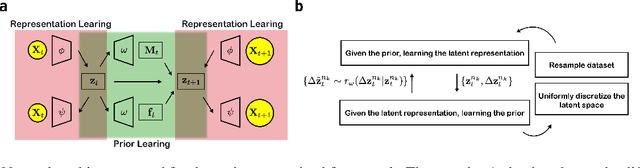
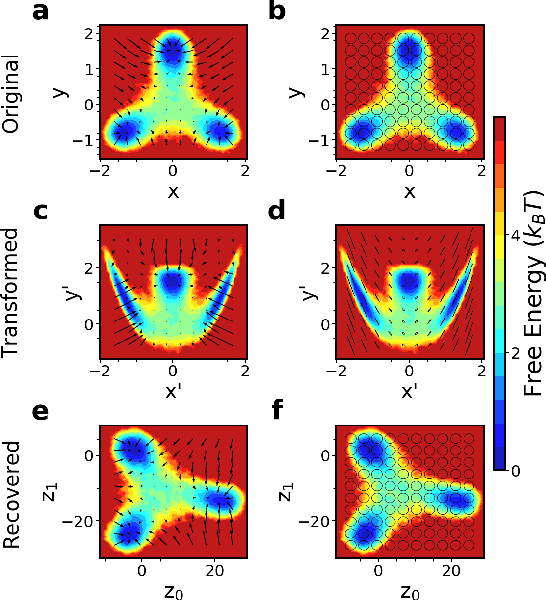

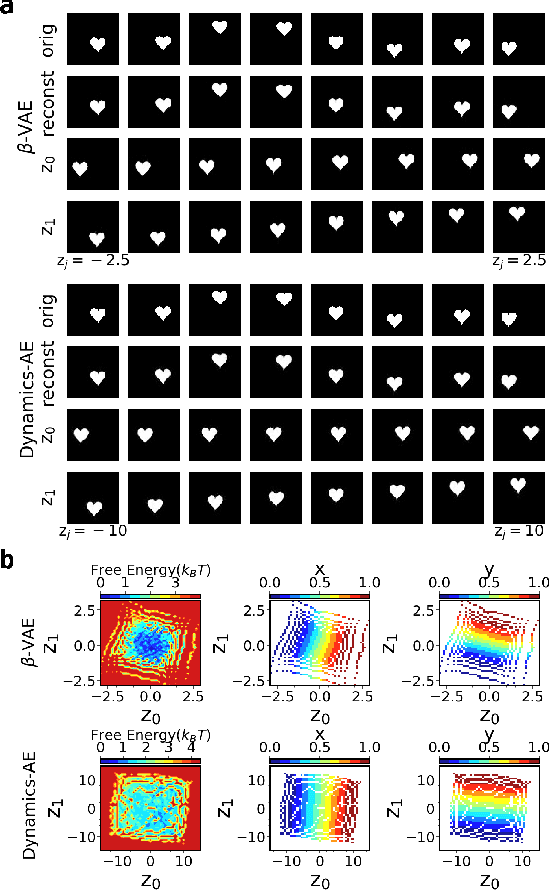
While representation learning has been central to the rise of machine learning and artificial intelligence, a key problem remains in making the learnt representations meaningful. For this the typical approach is to regularize the learned representation through prior probability distributions. However such priors are usually unavailable or ad hoc. To deal with this, we propose a dynamics-constrained representation learning framework. Instead of using predefined probabilities, we restrict the latent representation to follow specific dynamics, which is a more natural constraint for representation learning in dynamical systems. Our belief stems from a fundamental observation in physics that though different systems can have different marginalized probability distributions, they typically obey the same dynamics, such as Newton's and Schrodinger's equations. We validate our framework for different systems including a real-world fluorescent DNA movie dataset. We show that our algorithm can uniquely identify an uncorrelated, isometric and meaningful latent representation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge